Chứng minh các bất phương trình sau vô nghiệm x^2+√x+8 ≤ -3

Toán 10 Bài 2: Bất phương trình và hệ bất phương trình một ẩn

Bài 2 trang 88 Toán 10: Chứng minh các bất phương trình sau vô nghiệm

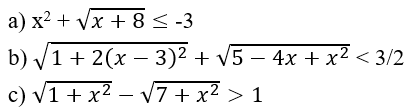
Trả lời

a) Vế trái: x² + √(x+8)≥ 0, mọi x ≥ -8

Vế phải: -3 < 0, mọi x

Suy ra tập xác định: D = ∅

Vậy bất phương trình vô nghiệm

b) 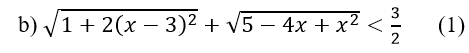(1)

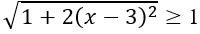
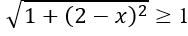
Vế trái: ,với mọi x

,với mọi x

Suy ra 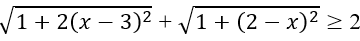,với mọi x

Vế phải: 3/2, mọi x. Mà 2 > 3/2

nên vế trái lớn hơn vế phải,với mọi x

Vậy bất phương trình vô nghiệm

c) Ta có 1 + x² < 7 + x² nên √(1+x² ) < √(7+x² )

Suy ra √(1+x² )-√(7+x² ) < 0 (1)

Theo đề bài √(1+x² )-√(7+x² ) > 1 (2)

Ta thấy, (1) và (2) mâu thuẫn với nhau

Do đó √(1+x² )-√(7+x² ) > 1 không xảy ra với mọi x

Vậy bất phương trình vô nghiệm.