Giải thích vì sao các cặp bất phương trình sau tương đương -4x + 1 > 0 và 4x – 1 < 0

Toán 10 Bài 2: Bất phương trình và hệ bất phương trình một ẩn

Bài 3 trang 88 Toán 10: Giải thích vì sao các cặp bất phương trình sau tương đương?

a) -4x + 1 > 0 và 4x – 1 < 0

b) 2x² + 5 ≤ 2x – 1 và 2x² – 2x + 6 ≤ 0

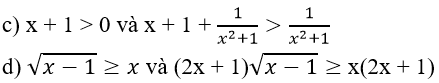
Trả lời

a) -4x + 1 > 0 ⇔ x < 1/4. Tập nghiệm: T = (-∞;1/4)

4x – 1 < 0 ⇔ x < 1/4. Tập nghiệm: T’ = (-∞;1/4)

Ta thấy T = T’. Vậy chúng tương đương.

b) 2x² + 5 ≤ 2x – 1 ⇔ 2x² – 2x + 6 ≤ 0 (1)

2x² – 2x + 6 ≤ 0 (2)

(1) và (2) có chung tập nghiệm. Vậy chúng tương đương.

c) x + 1 > 0 (1)

Biểu thức 1/(x²+1) > 0, mọi x

nên 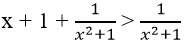(phép cộng)

Vậy x + 1 > 0 và 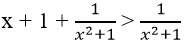tương đương.

d) √(x-1) ≥ x có tập xác định x ≥ 1

2x + 1 > 0 với x ≥ 1

nên (2x + 1)√(x-1) ≥ x(2x + 1) (phép nhân)

Vậy √(x-1) ≥ x và (2x + 1)√(x-1) ≥ x(2x + 1) tương đương.