Giải các bất phương trình sau 4x^2 – x + 1 < 0

---

Bài 5: Dấu của tam thức bậc hai

Bài 3 trang 105 Toán 10: Giải các bất phương trình sau:

a) 4x² – x + 1 < 0

b) -3x² + x + 4 ≥ 0

c) 1/(x²-4) < 3/(3x²+x-4)

d) x² – x – 6 ≤ 0

Trả lời

a) 4x² – x + 1 < 0

Xét f(x) = 4x² – x + 1

Δ = 1 – 16 < 0

a = 4 > 0

nên f(x) > 0, mọi x ∈ R.

Vậy bất phương trình vô nghiệm.

b) -3x² + x + 4 ≥ 0

Xét f(x) = -3x² + x + 4

f(x) = 0 ⇔ x1 = -1; x² = 4/3

Nên f(x) > 0 ⇔ -1 < x < 4/3

f(x) = 0 ⇔ x = -1; x = 4/3

Vậy tập nghiệm của bất phương trình: -1 ≤ x ≤4/3

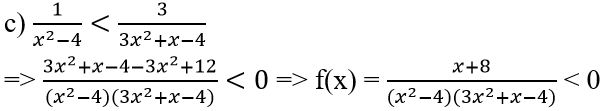
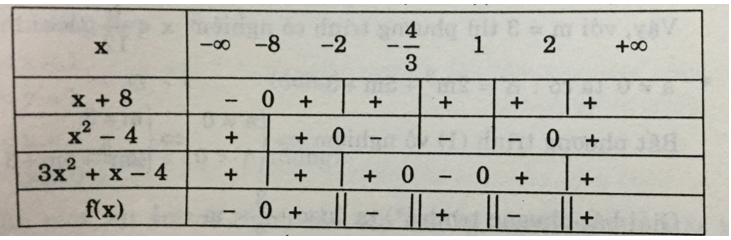
Nên f(x) < 0 ⇔ (x < -8); -2 < x < 4/3; 1 < x < 2

Vậy tập nghiệm của bất phương trình: (x < -8); -2 < x < 4/3; 1 < x < 2

d) x² – x – 6 ≤ 0

Xét f(x) = x² – x – 6

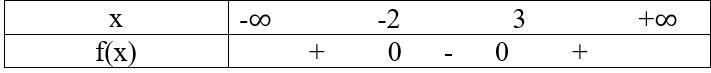
nên f(x) < 0 ⇔ -2 < x < 3

f(x) = 0 ⇔ x = -2; x = 3

Vậy tập nghiệm của bất phương trình: -2 ≤ x ≤ 3.