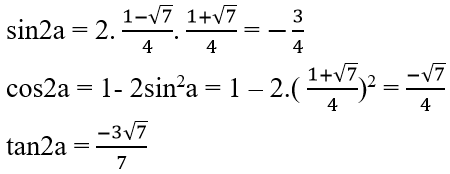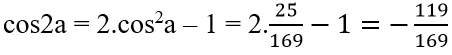Tính sin2a, cos2a, tan2a, biết sina = -0,6 và π < a < 3π/2

Bài 3: Công thức lượng giác

Bài 5 trang 154 Toán 10: Tính sin2a, cos2a, tan2a, biết:

a) sina = -0,6 và π < a < 3π/2

b) cosa = -5/13 và π/2 < a < π

c) sina+cosa = 1/2 và 3π/4 < a < π

Trả lời

a) sina = -0,6 và π < a < 3π/2

* sin2a = 2sinacosa (1) (công thức)

Mà π < a < 3π/2 ⇒ cosa < 0

và sina = -0,6 ⇒ cosa = -4/5

(1) ⇔ sin2a = 2. (-0,6). (-4/5) ⇔ sin2a = 24/25

* cos2a = 1 – 2sin2a = 1 – 2.(-3/5)2 = 1 – 18/25

cos2a – 7/25

* tan2a = sin2a/cos2a = 24/25.25/7 = 24/7

b) Vì π/2 < a < π nên sina > 0; tga < 0

và cosa = -5/13 nên sina = 12/13

Do đó,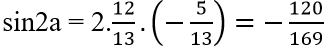

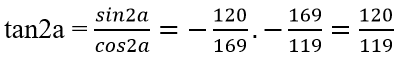
c) Vì 3π/4 < a < π nên sina > 0; cosa < 0

cos2a + sin2a = 1

sina + cosa = 1/2

⇒ cosa = (1-√7)/4; sina = (1+√7)/4

Suy ra: