Rút gọn các biểu thức sin(a + b).sin(a – b) = sin^2a – sin^2b = cos^2b – cos^2a

Bài 3: Công thức lượng giác

Bài 4 trang 154 Toán 10: Rút gọn các biểu thức:

Chứng minh các đẳng thức:

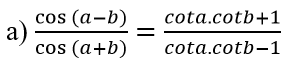
b) sin(a + b).sin(a – b) = sin²a – sin²b = cos²b – cos²a

c) cos(a + b).cos(a – b) = cos²a – sin²b = cos²b – sin²a

Trả lời

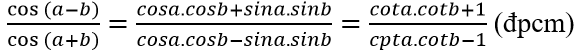
Chú ý: Có thể biến vế phải thành vế trái.

b) sin(a + b).sin(a – b) = sin²a – sin²b = cos²b – cos²a

= sin(a+b).sin(a-b)

= (sina.cosb + sinb.cosa).(sina.cosb – sinb.cosa)

= sin²a.cos²b – sin²b.cos²a

= sin²a(1-sin²b) – sin²b(1-sin²a)

= sin²a – sin²b (đpcm)

= 1 – cos²a – (1 – cos²b)

= cos²b – cos²a (đpcm)

c) cos(a + b).cos(a – b) = cos²a – sin²b = cos²b – sin²a

= cos(a + b) – cos(a-b)

= (cosa.cosb – sina.sinb)(cosa.cosb + sina.sinb)

= cos²a.cos²b – sin²a.sin²b

= cos²a – sin²b (đpcm)

= cos²b – sin²a (đpcm)