Cho hình hộp ABCD.A’B’C’D’. Chứng mình rằng hai mặt phẳng (BDA’) và (B’D’C’)

Bài 4: Hai mặt phẳng song song

Bài 3 trang 71 Toán 11: Cho hình hộp ABCD.A’B’C’D’

a) Chứng mình rằng: hai mặt phẳng (BDA’) và (B’D’C’) song song với nhau

b) Chứng minh rằng: đường chéo AC’ đi qua trọng tâm G₁ và G₂ của hai tam giác BDA’ và B’D’C’.

c) Chứng minh rằng: G₁,G₂ chia đoạn AC’ thành 3 phần bằng nhau.

d) Gọi O và I lần lượt là tâm của các hình bình hành ABCD và AA’C’C. xác định thiết diện của mặt phẳng (A’IO) với hình hộp đã cho.

Trả lời

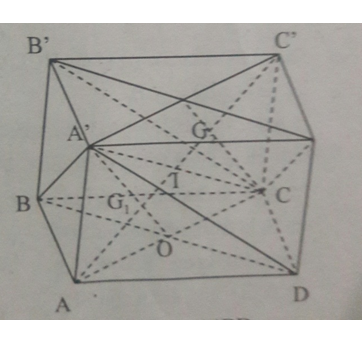
a) BB’D’D là hình bình hành ⇒ BD // B’D’

A’B’CD là hình bình hành ⇒ DA’ // B’C ⇒ (BD’A) // (B’D’C’)

b) Gọi O và I lần lượt là tâm của hình bình hành ABCD và AA’C’C.

Ta có O = AC ∩ BD ∈ (AA’C’C) ∩ (A’BD)

A’ ∈ (AA’C’C) ∩ (A’BD)

⇒ OA’ = (AA’C’C) ∩ (A’BD)

Gọi G₁= A’O ∩ AC’

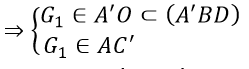
⇒ G₁ = AC' ∩ (A'BD)      (1)

Vì O, I là trung điểm của AC và A’C và A’O ∩ AI = G₁

⇒ G₁ là trọng tâm của ΔA’BD      (2)

Từ (1) và (2) suy ra AC’ cắt (A’BD) tai trọng tâm G₁ của ΔA’BD.

Tương tự AC’ cắt (B’D’C’) tai trọng tâm G₂ của ΔB’D’C’.

c) Theo câu b, ta có:

G₁, G₂ là trọng tâm ΔAA’C, ΔA’C’C

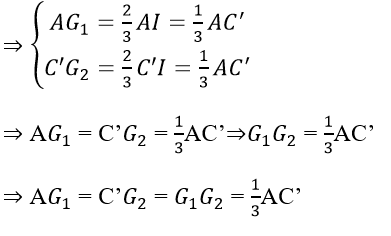
⇒ G₁ và G₁ chia đoạn AC’ thành ba phần bằng nhau.

d) Ta có : O,I lần lượt là tâm của ABCD và AA’C’C

Khi đó ta có: (A’IC’) ≡ (A’CO) ≡ (AA’C’C)

Dễ thấy thiết diện của hình hộp cắt bởi (A’IO) là hình bình hành AA’C’C.