Giải Toán 11 trang 71 Kết nối tri thức, Chân trời sáng tạo, Cánh diều

Haylamdo giới thiệu lời giải bài tập Toán 11 trang 71 Kết nối tri thức, Chân trời sáng tạo, Cánh diều sẽ giúp học sinh lớp 11 dễ dàng làm bài tập Toán 11 trang 71.

Giải Toán 11 trang 71 Kết nối tri thức, Chân trời sáng tạo, Cánh diều

- Toán lớp 11 trang 71 Tập 1 (sách mới):

• Giải Toán 11 trang 71 Chân trời sáng tạo

  Xem lời giải

• Giải Toán 11 trang 71 Cánh diều

  Xem lời giải

• Giải Toán 11 trang 71 Kết nối tri thức

  Xem lời giải

- Toán lớp 11 trang 71 Tập 2 (sách mới):

Lưu trữ: Giải Toán 11 trang 71 (sách cũ)

Bài 4 trang 71 Toán 11: Cho hình chóp S.ABCD. Gọi A₁ là trung điểm của cạnh SA và A₂ là trung điểm của cạnh AA₁. Gọi (α) và (β) là hai mặt phẳng song song với mặt phẳng (ABCD) và lần lượt đi qua A₁ và A₂. Mặt phẳng (α) cắt các cạnh SB,SC, SD lần lượt tại B₁, C₁, D₁. Mặt phẳng (β) cắt các cạnh SB, SC, SD lần lượt tại B₂, C₂, D₂. Chứng minh:

a) B₁, C₁, D₁ lần lượt là trung điểm của các cạnh SB, SC, SD.

b) B₁B₂ = B₂B, C₁C₂ = C₂C, D₁D₂=D₂D

c) Chỉ ra các hình chóp cụt có một đáy là tứ giác ABCD.

Trả lời

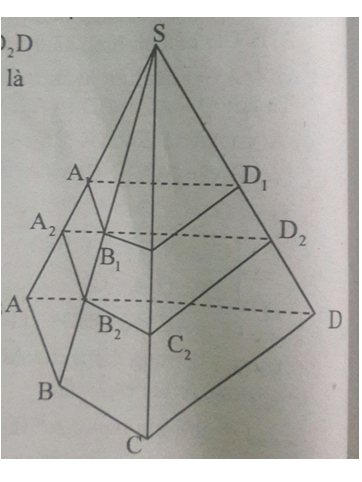
a) Theo bài ra ta có: (α) // (ABCD)

(SAB) ∩ (α) = A₁ B₁

(SAB) ∩ (ABCD) = AB

⇒A₁B₁ // AB

Mặt khác A₁ là trung điểm của SA

⇒A₁B₁ là đường trung bình của ΔSAB

⇒B₁ là trung điểm của SB

Tương tự ta có B₁C₁ // BC và B₁ là trung điểm của SB

⇒C₁ là trung điểm của SC

Tương tự ta có C₁D₁ // CD và C₁ là trung điểm của SC

⇒D₁ là trung điểm của SD

Vậy B₁, C₁, D₁ lần lượt là trung điểm của các cạnh SB, SC, SD.

Theo bài ra ta có:

(α) // (β) // (ABCD)

SA, SB lần lượt căt (α), (β), (ABCD) tại A₁, A₂, A và B₁, B₂, B

Theo định lý Ta-let, ta có:

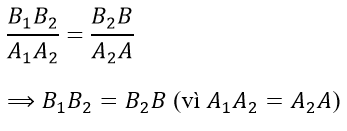
SA, SC lần lượt căt (α), (β), (ABCD) tại A₁, A₂, A và C₁, C₂, C

Theo định lý Ta-let, ta có:

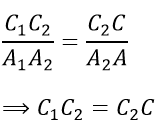
SA, SD lần lượt căt (α), (β), (ABCD) tại A₁, A₂, A và D₁, D₂, D

Theo định lý Ta-let, ta có:

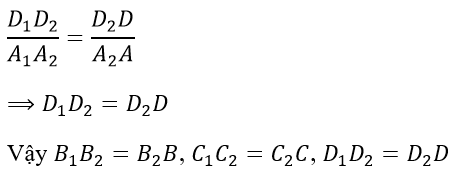
c) Các hình chóp cụt có 1 đáy là tứ giác ABCD là:

A₁B₁C₁D₁.ABCD và A₂B₂C₂D₂.ABCD