Chứng minh rằng phương trình 2x^3 – 6x + 1= 0 có ít nhất hai nghiệm

Bài 3: Hàm số liên tục

Bài 6 trang 141 Toán 11: Chứng minh rằng phương trình

a) 2x³ – 6x + 1= 0 có ít nhất hai nghiệm.

b) cosx = x có nghiệm

Trả lời

a) Đặt f(x) = 2x³ – 6x + 1 = 0, hàm số này liên tục trên R.

Ta có: f(–2) = –3, f(1) = –3, f(0) = 1. Từ đó ta có:

+ f(–2). f(0) = –3 < 0 ⇒ ∃ ít nhất một số x₁ ∈ ( –2; 0) sao cho f(x₁) = 0 hay phương trình f(x) = 0 có ít nhất một nghiệm thuộc ( –2;0).

+ f(0).f(1) = –3 < 0 ⇒ ∃ ít nhất một số x₂ ∈ (0; 1)

Như vậy phương trình f(x) = 0 có ít nhất hai nghiệm.

b) Đặt g(x) = x – cosx, hàm số này liên tục trên R.

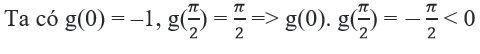
⇒ Phương trình g(x) = 0 có ít nhất một nghiệm x ∈ (0; π/2)

⇒ Phương trình cosx = x có nghiệm