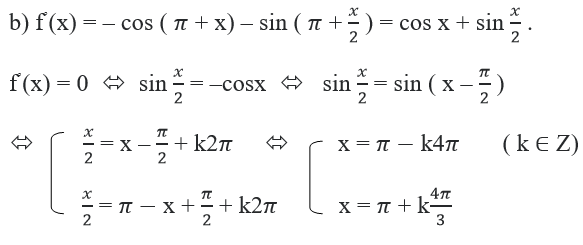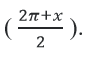Giải phương trình f’(x) = 0, biết rằng f(x) = 3cosx + 4sinx + 5x

Bài 3: Đạo hàm của hàm số lượng giác

Bài 7 trang 169 Toán 11: Giải phương trình f’(x) = 0, biết rằng:

a) f(x) = 3cosx + 4sinx + 5x

b) f(x) = 1 – sin(π + x) + 2cos

Trả lời

a) f’(x) = – 3sinx + 4cosx + 5

f’(x) = 0 ⇔ 3/(5 ) sinx – 4/5 cos = 1 (1)

Đặt cosφ = 3/5 ( φ ∈ (0; π/2 )) ⇒ sinφ = 4/5 , ta có:

(1) ⇔ sinxcosφ – cosxsinφ = 1

⇔ sin(x – φ ) = sin π/2 ⇔ x = φ + π/2 + k2π ; k ∈ Z.