Từ một hộp chứa 5 quả cầu được đánh số 1, 2, 3, 4, 5 lấy ngẫu nhiên liên tiếp

Bài 4: Phép thử và biến cố

Bài 7 trang 64 Toán 11: Từ một hộp chứa 5 quả cầu được đánh số 1, 2, 3, 4, 5 lấy ngẫu nhiên liên tiếp hai lần mỗi lần một quả và sắp xếp theo thứ tự từ trái sang phải.

a) Xây dựng không gian mẫu

b) Xác định các biến cố:

A: “Chữ số sau lớn hơn chữ số trước”;

B: “Chữ số trước gấp đôi chữ số sau”;

C: “Hai chữ số bằng nhau”

Trả lời

a) Khi lấy ngẫu nhiên liên tiếp hai quả cầu ta có quả cầu lấy lần một được đán số i, quả cầu lấy lần hai được đánh số là j (i, j = 1, 2, 3, 4, 5, i ≠ j)

Ta kí hiệu bộ hai quả cầu này là (i;j). Khi đó không gian mẫu là:

Ω = {(i; j)\i, j = 1, 2, 3, 4, 5; i ≠ j}

Hiển nhiên n(Ω) =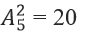

b) Ta có: A = {(i; j)\i, j = 1, 2, 3, 4, 5; i < j}

= {(1,2), (1,3), (1,4), (1,5), (2,3), (2,4), (2,5) , (3,4), (3,5), (4,5)}

Khi đó n(A) = 10

* B = {(2i,i) \ i = 1, 2, 3, 4, 5; 2i ≤ 4 = {(2,1); (4,2)}

* C = ∅ vì chỉ có 5 quả cầu đánh số 1, 2, 3, 4, 5 nên đã lấy ra quả đánh số i thì không thể còn quả đánh số i trong hộp nữa và do đó rút lần 2 không thể được quả đánh số i.