Trên mỗi hình 105,106,108 các tam giác vuông nào bằng nhau. Vì sao

Giải bài tập Toán lớp 7 Luyện tập (trang 124)

Bài 39 trang 124 Toán lớp 7 Tập 1: Bài 39 trang 124 Hình học 7

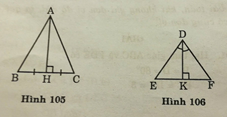
Trả lời

- Hình 105

Hai tam giác vuông AHB và AHC có:

AH cạnh chung

HB = HC (gt)

Vậy ΔABH = ΔACH (c.g.c)

- Hình 106

Hai tam giác vuông DKE và DKF có:

EDK = FDK (gt)

DK là cạnh chung.

Vậy ΔDKE = ΔDKF (g.c.g)

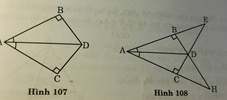
- Hình 107

Hai tam giác vuông ABD và ACD có:

AD cạnh huyền chung

BAD = CAD (gt)

Vậy: ΔABD = ΔACD (g.c.g)

- Hình 108

+) Hai tam giác vuông ABD và ACD có:

AD cạnh huyền chung

BAD = CAD (gt)

Suy ra: ΔABD = ΔACD (ch.gn)

+) Hai tam giác vuông ABH và ACE có

BAC là góc chung

AB = AC ( do ΔABD = ΔACD)

B = C = 90⁰

Suy ra: ΔABH = ΔACE (g.c.g)

+) Hai tam giác vuông DBE và DCH có:

B = C = 90⁰

DB = DC (do ΔABD = ΔACD)

BDE = CDH (hai góc đối đỉnh)

Suy ra: ΔDBE = ΔDCH (g.c.g)