Cho tam giác ABC có A = 90^0, kẻ AH vuông góc với BC (H ∈ BC)

Giải bài tập Toán lớp 7 Luyện tập (trang 124)

Bài 42 trang 124 Toán lớp 7 Tập 1: Cho tam giác ABC có A = 90⁰, kẻ AH vuông góc với BC (H ∈ BC). Các tam giác AHC và BAC có AC là cạnh chung, C là góc chung, AHC = BAC = 90⁰, nhưng hai tam giác không bằng nhau.

Tại sao ở đây không áp dụng trường hợp góc cạnh góc để kết luận ΔAHC = ΔBAC?

Trả lời

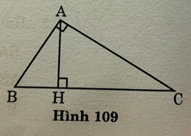
Xét tam giác AHC có AHC = 90⁰ và C kề với cạnh HC (g.c.g)

Xét tam giác BAC có BAC = 90⁰ và C kề với cạnh AC (g.c.g)

Trong tam giác AHC có HC không bằng AC

Do đó ta không thể áp dụng trường hợp góc – cạnh – góc để kết luận ΔAHC = ΔBAC.