Bài 11 trang 42 Toán 9 Tập 2

Bài 3: Phương trình bậc hai một ẩn

Bài 11 trang 42 Toán 9 Tập 2: Đưa các phương trình sau về dạng ax² + bx + c = 0 và chỉ rõ các hệ số a, b, c

a) 5x² + 2x = 4 – x

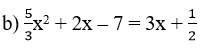
c) 2x² + x - √3 = √3x + 1

d) 2x² – 2(m – 1)x + m² = 0, m là một hằng số

Bài giải:

a) 5x² + 2x = 4 – x

⇔ 5x² + 2x + x – 4 = 0 (đưa về dạng ax² + bx + c =0)

⇔ 5x² + 3x – 4 = 0; các hệ số a = 5; b = 3; c = -4

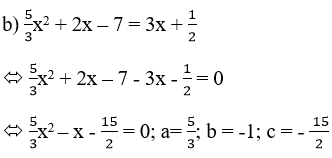
Chú ý:

1. Đến đây, ta có thể qui đồng mẫu để có dạng: 10x² – 6x – 45 = 0; lúc này a = 10; b = -6; c= -45

2. Khi lấy một hệ số, ta lấy số và lấy luôn cả dấu trước nó.

c) 2x² + x - √3 = √3x + 1

⇔ 2x² + x - √3 - √3x – 1 = 0

⇔ 2x² + (1- √3)x – (√3 – 1) = 0: a = 2; b = 1- √3; c = - (√3 – 1)

d) 2x² – 2(m – 1)x + m² = 0, m là một hằng số

⇔ 2x² -2(m – 1)x + m² = 0: a = 2; b = -2(m-1); c = m²

Chú ý:

1. Trong các hệ số, không có ẩn x

2. Chữ m ở đây biểu thị một số cho sẵn (còn gọi là tham số).