Bài 12 trang 42 Toán 9 Tập 2

Bài 3: Phương trình bậc hai một ẩn

Bài 12 trang 42 Toán 9 Tập 2: Giải các phương trình sau:

a) x² – 8 = 0

b) 5x² – 20 = 0

c) 0,4x² + 1 = 0

d) 2x² + √2x = 0

e) -0,4x² + 1,2x = 0

Bài giải:

a) x² – 8 = 0 (dạng ax² + bx + c = 0 với a = 1; b = 0; c = -8)

Bước 1: Phân tích vế trái thành nhân tử:

x² – 8 = x² – (2√2)² = (x + 2√2)(x - 2√2)

Bước 2: Đưa x² – 8 = 0 về phương trình tích:

x² – 8 = 0 ⇔ (x + 2√2)(x - 2√2) = 0

⇔ (x + 2√2) = 0 hoặc (x - 2√2) = 0

⇔ x = -2√2 hoặc x = 2√2

Vậy phương trình có nghiệm là x = -2√2 hoặc x = 2√2

b) 5x² – 20 = 0

⇔ 5(x² – 4) = 0 ⇔ x² - 4 = 0 ⇔ (x-2)(x + 2) = 0

⇔ x = 2 hoặc x = -2

Vậy phương trình có nghiệm x = 2 hoặc x = -2

c) 0,4x² + 1 = 0 (dạng ax² + bx + c = 0 với a = 0,4; b = 0; c = 1)

Ta thấy 0,4x² ≥ 0 với mọi x ∈ R

1 > 0 với mọi x ∈ R

nên 0,4x² + 1 > 0 với mọi x ∈ R, do đó không có giá trị của x để cho 0,4x² + 1= 0

Vậy phương trình đã cho vô nghiệm

Chú ý: Trước khi giải phải chú ý quan sát kỹ:

1. Các hệ số a, b, c của phương trình đã cho.

2. Xem vế trái có bằng 0 được không.

d) 2x² + √2x = 0 (dạng ax² + bx + c = 0 với a = 2; b = √2; c = 0)

⇔ x(2x + √2) = 0 (cẩn thận √2x chứ không phải )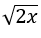

⇔ x = 0 hoặc 2x + √2 = 0 ⇔ x = 0 hoặc x = -

e) -0,4x² + 1,2x = 0 (dạng ax² + bx + c = 0 với a = -0,4; b =1,2; c = 0)

⇔ x (-0,4x + 1,2) = 0 ⇔ x = 0 hoặc -0,4x + 1,2 = 0

⇔ x = 0 hoặc x = 3

Vậy phương trình có nghiệm x = 0 hoặc x = 3

Chú ý: Học sinh phân biệt phương trình: 0,4x² + 1 =0 (câu c) và -0,4x² + 1,2 = 0(câu e)

để hiểu rõ về loại phương trình này.