Bài 26 trang 115 Toán 9 Tập 1

Bài 6: Tính chất của hai tiếp tuyến cắt nhau

Bài 26 trang 115 Toán 9 Tập 1: Cho đường tròn (O), điểm A nằm bên ngoài đường tròn. Kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm).

a) Chứng minh rằng OA vuông góc với BC.

b) Vẽ đường kính CD. Chứng minh rằng BD song song với AO.

c) Tính độ dài các cạnh của tam giác ABC biết OB = 2cm, OA = 4cm.

Bài giải:

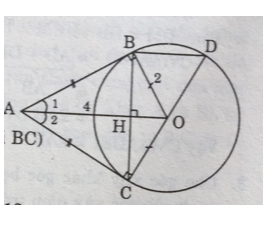
a) OA ⊥ BC

Ta có: OB = OC = bán kính     (1)

AB = AC (hai tiếp tuyến cắt nhau tại A)     (2)

Từ (1) và (2) suy ra OA là trung trực của BC.

Vậy OA ⊥ BC

BD//AO

tam giác BCD nội tiếp đường tròn (O) có CD là đường kính nên tam giác BCD vuông ở B hay:

BD ⊥ BC

Ta có: OA ⊥ BC (câu a)

⇒ BD // OA (cùng vuông góc với BC)

Độ dài các cạnh của tam giác ABC

tam giác OAB vuông tại B

⇒ AB² = OA² - OB² = 4² – 2² = 12

⇒ AB = √12 = 2√3

⇒ AB = AC = 2√3 cm

tam giác OAB vuông tại B, đường cao BH

⇒ BH . OA = OB . AB

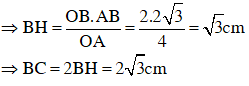
Vậy các cạnh của tam giác ABC là:

AB = AC = BC = 2√3 (cm)

* Cách tính khác:

Tam giác OAB có góc B = 90° ; OB = 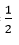OA = (2cm)

⇒ Tam giác OAB là nửa tam giác đều.

⇒ Góc A₁ =30°

theo tính chất hai tiếp tuyến cắt nhau tại A

⇒ ∠A₁ = ∠A₂ = 30° ⇒ ∠BAC = 60°     (1)

và AB = AC     (2)

Từ (1) và (2) suy ra tam giác ABC là tam giác đều ⇒ AB = AC = BC

mà AB² = OA² - OB² = 4² - 2² = 12 ⇒ AB = √12=2√3(cm)

Vậy AB = AC = BC = 2√3 (cm)