Bài 27 trang 115 Toán 9 Tập 1

Bài 6: Tính chất của hai tiếp tuyến cắt nhau

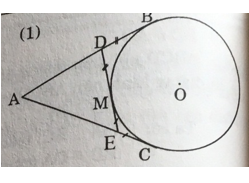
Bài 27 trang 115 Toán 9 Tập 1: Từ một điểm A nằm bên ngoài đường tròn (O), kẻ các tiếp tuyến AB, AC với đường tròn (B, C là các tiếp điểm). Qua điểm M thuộc cung nhỏ BC, kẻ tiếp tuyến với đường tròn (O), nó cắt các tiếp tuyến AB và AC theo thứ tự ở D và E. Chứng minh rằng chu vi tam giác ADE bằng 2AB.

Bài giải:

• CV (tam giác ADE) = 2AB:

Theo tính chất của hai tiếp tuyến cắt nhau

Ta có: AB = AC; DB = DM ; EC = EM

CV(tam giác ADE) = AD + DM + EM + AE     (1)

Thay DM = DB và EM = EC vào (1)

CV(tam giác ADE) = AD + DB + EC + AE = AB + AC = 2AB (vì AB = AC)

Vậy CV(AADE) = 2AB