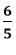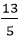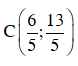Bài 37 trang 61 Toán 9 Tập 1

Ôn tập chương 2

Bài 37 trang 61 Toán 9 Tập 1:

a) Vẽ đồ thị hai hàm số sau trên cùng một mặt phẳng tọa độ: y = 0,5x + 2 (1);    y = -2x + 5 (2).

b) Gọi giao điểm của đường thẳng y = 0,5x + 2 và y = 5 - 2x và với trục hoành theo thứ tự là A, B và gọi giao điểm của hai đường thẳng đó là C. Tìm tọa độ của các điểm A, B, C.

c) Tính các khoảng cách AB, AC và BC (theo đơn vị đo trên trục tọa độ là xentimet) (làm tròn đến chữ số thập phân thứ hai).

d) Tính các góc tạo bởi các đường thẳng có phương trình (1) và (2) với trục Ox (làm tròn đến phút).

Bài giải:

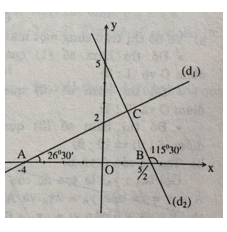
a) Vẽ đồ thị:

Đường thẳng (d₁): y = 0,5x + 2 đi qua điểm (0 ; 2) và điểm (-4 ; 0)

Đường thẳng (d₂): y = -2x + 5 đi qua điểm (0; 2) và điểm (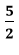 ; 0).

b) Tọa độ của A, B: A(-4; 0) ; B(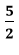 ; 0).

Tọa độ của C

C là giao điểm của (d₁) và (d₂) nên:

C ∈ (d₁) ⇔ 0,5x_C + 2 = y_C

C ∈ (d₂) ⇔ y_C = 5 - 2x_C

Suy ra, 0,5x_C + 2 = 5- 2x_C < ⇒ x_C =

Vì y_C = 5 - 2x_C nên y_C =

Vậy,

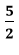
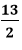
c) Khoảng cách: AB = AO + OB = 4 + = cm = 6,5 cm

    AC = 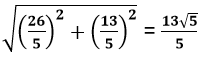cm = 5,82 cm

    CB = 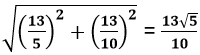cm = 2,30 cm

d) Tính góc tạo bởi các đường thẳng và trục Ox

- Gọi a là góc tạo bởi đường thẳng cố phương trình (1) và trục Ox, ta có tg α = 0,5

⇒ α ≈ 26^o40’

- Gọi β là gốc tạo bởi đường thẳng có phương trình (2) và trục Ox, ta có tgβ = -2.

Mà tgβ’ = 2 ⇒ β' = 64^o30' nên β = 180^o - 64^o30’

Vậy, β = 115^o30'