Bài 41 trang 128 Toán 9 Tập 1

Ôn tập chương 2

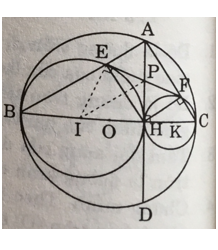
Bài 41 trang 128 Toán 9 Tập 1: Cho đường tròn (O) có đường kính BC, dây AD vuông góc với BC tại H Gọi E, F theo thứ tự là chân các đường vuông góc kẻ từ H đến AB, AC. Gọi (I), (K) theo thứ tự là các đường tròn ngoại tiếp tam giác HBH, HCF.

a) Hãy xác định vị trí tương đối của các đường tròn: (I) và (O), (K) và (O), (I) và (K).

b) Tứ giác AEHF là hình gì? Vì sao?

c) Chứng minh đẳng thức AE.AB = AF.AC

d) Chứng minh rằng EF là tiếp tuyến chung của hai đường tròn (I) và (K)

e) Xác định vị trí của điểm H để EF có độ dài lớn nhất.

Bài giải:

a) * (I) và (*)

Ta có: IO = BO – HI     (1)

Mà IO là đoạn nối tâm của (I) và (K);

r = BI là bán kính của (I);

R = BO là bán kính của (O)

Từ (1), ta có: IO = R - r

Vậy, (I) và (O) tiếp xúc

* (K) và (O)

Tương tự, OK là đoạn nối tâm của (K) và (O);

HK = r₁ là bán kính của (K) và OC = R là bán kính của (O).

Mà OK = OC - CK ⇔ OK = R – r₁.

Vậy, (K) và (O) tiếp xúc trong với nhau.

* (I) và(K)

Ta có: IK = IH + HK. Mà IH = r và HK = r₁ nên IK = r + r₁

Vậy, (I) và (K) tiếp xúc ngoài với nhau.

b) AEHF là hình gì ? Tại sao ?

AEHF có: ∠A = 90° (ΔABC nội tiếp trong nửa đường tròn đường kính BC)

∠E = ∠F = 90° (gt)

Vậy, AEHF là hình chữ nhật.

c) Chứng minh AE.AB = AF.AC

* ΔAHB vuông tại H có HE là đường cao ⇒ AH² = AB . AE     (1)

* ΔAHC vuông tại H, có HF là đường cao ⇒ AH² = AC . AF     (2)

(1) và (2) ⇒ AE.AB = AF.AC

d) Chứng minh rằng EF là tiếp tuyến chung của hai đường tròn (I) và (K).

Gọi P là giao điểm của AH và EF. Vì AH và EF là hai đường chéo của hình chữ nhật AEHF (cmt) nên PA = PE = PH.

Mặt khác ΔPHI và ΔPEI bằng nhau (c.c.c) ⇒ góc IEP = góc IHP

Mà ∠PHI = 90° nên ∠PEI = 90°. Suy ra PE là tiếp tuyến của (I) tại E

Tương tự, PF vuông góc với KF tại F. Suy ra PF là tiếp tuyến của (K) tại F.

Vậy, EF là tiếp tuyến chung của (I) và (K).

e) Xác định vị trí của điểm H để EF có độ dài lớn nhất

Ta đã có: EF = AH (AEHF là hình chữ nhật) nên EF có độ dài lớn nhất ⇔ AH có độ dài lớn nhất.

Mà AD = 2AH. (AD là dây của (O)) nên

AH lớn nhất ⇔ AD lớn nhất ⇔ AD là đường kính ⇔ H trùng với O.

Tóm lại, EF có độ dài lớn nhất ⇔ H trùng với O.