Bài 42 trang 128 Toán 9 Tập 1

Ôn tập chương 2

Bài 42 trang 128 Toán 9 Tập 1: Cho hai đường tròn (O) và (O’) tiếp xúc ngoài tại A, BC là tiếp tuyến chung ngoài, B ∈ (O), C ∈ (O’). Tiếp tuyến chung trong tại A cắt BC ở điểm M. Gọi E là giao điểm của OM và AB, F là giao điểm của O’M và AC. Chứng minh rằng :

a) Tứ giác AEMF là hình chữ nhật.

b) ME.MO = MF.MO’

c) OO’ là tiếp tuyến của đường tròn có đường kính là BC.

d) BC là tiếp tuyến của đường tròn có đường kính là OO’.

Bài giải:

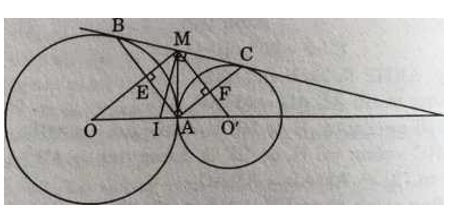
a) Chứng minh AEMF là hình chữ nhật

MB và MA là hai tiếp tuyến của (O) cùng phát xuất từ M nên MO vuông góc với AB tại E. Tương tự MF ⊥ AC tại F.

Mặt khác, MO là phân giác của ∠BMA

MO' là phân giác của ∠CMA

∠MBA kề bù ∠CMA

⇒ ∠EMF = 90°

Tứ giác AEMF có ∠E = ∠M = ∠F = 90° nên AEMF là hình chữ nhật.

b) ME.MO = MF.MO' (xem câu b, bài 1)

c) OO' là tiếp tuyến của đường tròn đường kính BC.

Vì AEMF là hình chữ nhật nên ∠BAG= 90°.     (1)

∆ABC có MA = MB (tiếp tuyến phát xuất từ M của (O)).

và MB = MC (tương tự) nên M là trung điểm của BC     (2)

Từ (1) và (2) ⇒ đường tròn có đường kính BC đi qua A.

Mà MA vuông góc với OO' tại A (MA là tiếp tuyến chung) nên OO' vuông góc với bán kính MA tại A của đường tròn đườa kính BC. Vậy, OO' là tiếp tuyến của đường tròn có đường kính BC.

BC là tiếp tuyến của đường tròn cổ đường kính là OO’.

Gọi I là trung điểm của OO’' thì IM = 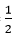OO'

và IM vuông góc với BC tại M (đường trung bình của hình thang OBCO' vuông tại B và C).

Tóm lại, BC vuông gócc với bán kính IM tại M cửa đường tròn tâm I, bán kính IM. Đây chính là đường tròn đường kính OO'.

Vậy, BC tiếp xúc với đường tròn đường kính OO'.