Bài 7 trang 69 Toán 9 Tập 1

Luyện tập (trang 69-70)

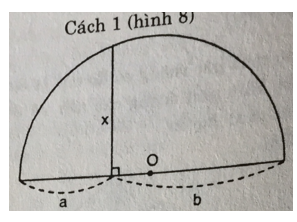
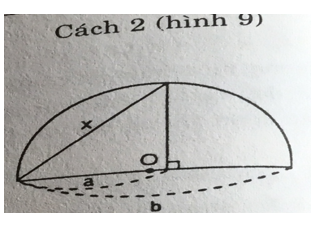
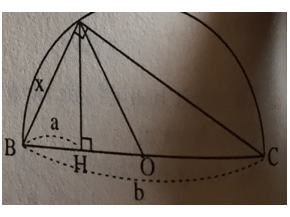
Bài 7 trang 69 Toán 9 Tập 1: Người ta đưa ra hai cách vẽ đoạn trung bình nhân x của hai đoạn thẳng a, b (tức là x² = ab) như trong hai hình sau:

Dựa vào hệ thức (1) và (2), hãy chứng minh các cách dựng trên là đúng.

Gợi ý: Nếu một tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh đó thì tam giác ấy là tam giác vuông.

Bài giải:

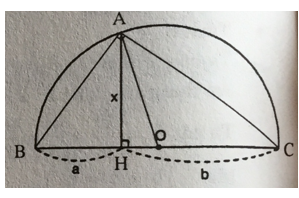
Cách 1:

OA = OB = OC (=bán kính)

⇒ AO = 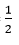BC ⇒ tam giác ABC vuông tại A

Mà AH là đường cao ứng với cạnh huyền BC nên AH² = BH.HC

Trong đó: AH = x;    BH = a;    HC = b (gt)

Vậy, x² = ab (đpcm)

Cách 2:

Chứng minh tương tự cách 1, ta có:

Tam giác ABC vuông tại A có đường cao AH ⇒ AB² = BH.BC

Mà AB = x;    BH = a;    BC = b (gt)

nên x² = ab (đpcm)

Tóm lại: Cả hai cách dựng ở hai hình 8 và 9 đều đúng.