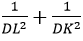Bài 9 trang 70 Toán 9 Tập 1

Luyện tập (trang 69-70)

Bài 9 trang 70 Toán 9 Tập 1: Cho hình vuông ABCD. Gọi I là điểm nằm giữa A và B. Tia DI và CB cắt nhau tại K. Kẻ đường thẳng qua D vuông góc với DI, cắt đường thẳng BC tại L. Chứng minh rằng:

a) Tam giác DIL là một tam giác cân.

b) Tổng 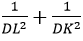không đổi khi I thay đổi trên cạnh AB.

Bài giải:

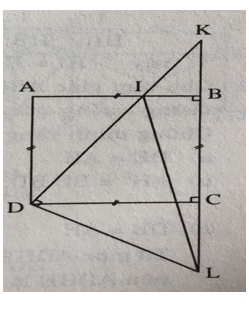
a) Tam giác DIL là tam giác cân:

Hai tam giác vuông DAI và DCL có:

AD = CD (cạnh hình vuông)

∠ADI= ∠CDL (cùng phụ với góc ∠IDC)

⇒ tam giác DAI = tam giác DCL (cạnh huyền, góc nhọn)

⇒ DI = DL

Do đó tam giác DIL cân ở D.

b) 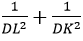: không đổi

tam giác DLK có ∠LDK = 90^o (gt), DC ⊥ LK (gt)

⇒ tam giác DLK vuông ở D có đường cao DC.

Áp dụng hệ thức 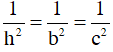(1)

Trong đó h =DC;    b = DK;    c = DL

(1) ⇒

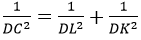
Mà DC là cạnh hình vuông ABCD nên không đổi.

Vậy, tổng không đổi khi I thay đổi trên cạnh AB.