Viết phương trình tiếp tuyến của đường tròn (C) có phương trình x^2 + y^2 - 8x - 6y = 0 biết rằng tiếp tuyến

Bài 2: Phương trình đường tròn

Bài 3.26 trang 156 Sách bài tập Hình học 10: Viết phương trình tiếp tuyến của đường tròn (C) có phương trình x² + y² - 8x - 6y = 0 biết rằng tiếp tuyến đó đi qua gốc tọa độ O.

Lời giải:

    Đường tròn (C): x² + y² - 8x - 6y có tâm I(4;3) và bán kính R = 5.

    Cách 1: xét đường thẳng Δ đi qua gốc tọa độ O và có hệ số góc k, Δ có phương trình y - kx = 0

    Ta có: Δ tiếp xúc với (C) ⇔ d(I, Δ) = R

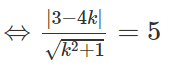
    ⇔ (3 - 4k)² = 25(k² + 1)

    ⇔ 9 - 24k + 16k² = 25k² + 25

    ⇔ 9k² + 24k + 16 = 0

    ⇔ k = -4/3

    Vậy ta được phương trình tiếp tuyến là: y + 4x/3 = 0 hay 4x + 3y = 0

    Cách 2: Do tọa độ O(0;0) thỏa mãn phương trình của (C) nên điểm O nằm trên (C). Tiếp tuyến với (C) tại O có vectơ pháp tuyến

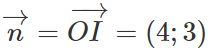
    Suy ra Δ có phương trình: 4x + 3y = 0.