Cho đường tròn (C): (x + 1)^2 + (y - 2)^2 = 9 và điểm M(2;-1). Chứng tỏ rằng qua M ta vẽ được

Bài 2: Phương trình đường tròn

Bài 3.25 trang 156 Sách bài tập Hình học 10: Cho đường tròn (C): (x + 1)² + (y - 2)² = 9 và điểm M(2;-1).

    a) Chứng tỏ rằng qua M ta vẽ được hai tiếp tuyến Δ₁ và Δ₂ với (C), hãy viết phương trình của Δ₁ và Δ₂.

    b) Gọi M₁ và M₂ lần lượt là hai tiếp điểm của Δ₁ và Δ₂ với (C) , hãy viết phương trình của đường thẳng d đi qua M₁ và M₂

Lời giải:

    a) (C) có tâm I(-1; 2) và có bán kính R = 3. Đường thẳng đi qua M(2; -1) và có hệ số góc k có phương trình:

    y + 1 = k(x - 2) ⇔ kx - y - 2k - 1 = 0

    Ta có: Δ tiếp xúc với (C) ⇔ d(I; Δ ) = R

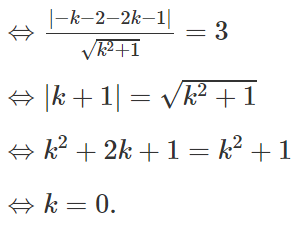
    Vậy ta được tiếp tuyến Δ₁: y + 1 = 0

    Xét đường thẳng Δ₂ đo qua M(2;-1) và vuông góc với Ox, Δ₂ có phương trình x - 2 = 0. Ta có:

    d(I; Δ ) = |-1 - 2| = 3 = R

    Suy ra Δ₂ tiếp xúc với (C) .

    Vậy qua điểm M ta vẽ được hai tiếp tuyến với (C), đó là:

    Δ₁: y + 1 = 0 và Δ₂: x - 2 = 0

    b) Δ₁ tiếp xúc với (C) tại M₁(-1; -1)

    Δ₂ tiếp xúc với (C) tại M₂(2; 2)

    Phương trình của đường thẳng d đi qua M₁ và M₂ là: x - y = 0.