Cho hai đường tròn (C1): x^2 + y2 - 6x + 5 = 0 và (C2): x^2 + y2 - 12x - 6y + 44 = 0. Tìm câm và bán kính

Bài 2: Phương trình đường tròn

Bài 3.27 trang 156 Sách bài tập Hình học 10: Cho hai đường tròn (C₁): x² + y₂ - 6x + 5 = 0 và (C₂): x² + y₂ - 12x - 6y + 44 = 0

    a) Tìm câm và bán kính của (C₁) và (C₂) .

    b) Lập phương trình tiếp tuyến chung của (C₁) và (C₂).

Lời giải:

    a) (C₁) có tâm có bán kính R₁ = 2;

    (C₂) có tâm có bán kính R₂ = 1.

    b) Xét đường thẳng Δ có phương trình:

    y = kx + m hay kx - y + m = 0. Ta có:

    Δ tiếp xúc với (C₁) và (C₂) khi và chỉ khi

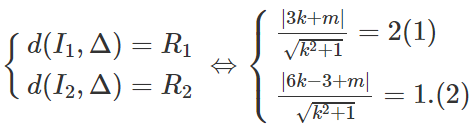
    Từ (1) và (2) suy ra

    |3k + 2| = 2|6k - 3 + m|

    Trường hợp 1: 3k + m = 2(6k - 3 + m) ⇔ m = 6 - 9k (3)

    Thay vào (2) ta được

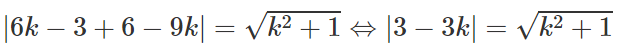
    ⇔ 9 - 18k + 9k² = k² + 1

    ⇔ 8k² - 18k + 8 = 0

    ⇔ 4k² - 9k + 4 = 0

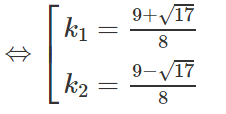
    Thay giá trị của k vào (3) ta tính được

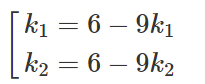
    Vậy ta được hai tiếp tuyến

    Δ₁: y = k₁x + 6 - 9k₁

    Δ₂: y = k₂x + 6 - 9k₂

    Trường hợp 2:

    3k + m = -2(6k - 3 + m)

    ⇔ 3m = 6 - 15k

    ⇔ m = 2 - 5k (4)

    Thay vào (2) ta được

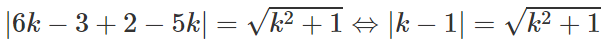
    ⇔ (k - 1)² = k² + 1

    ⇔ k² - 2k + 1 = k² + 1

    ⇔ k = 0

    Thay giá trị của k vào (4) ta được m = 2.

    Vậy ta được tiếp tuyến Δ₃: y = 2

    Xét đường thẳng Δ₄ vuông góc với Ox tại x₀:

    Δ₄: x - x₀ = 0

    Δ₄ tiếp xúc vơi (C₁) và (C₂) khi và chỉ khi

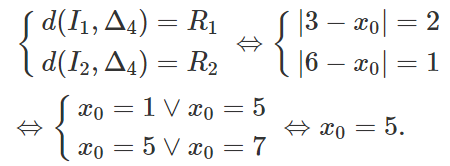
    Vậy ta được tiếp tuyến: Δ₄: x - 5 = 0

    Tóm lại hai đường tròn (C₁) và (C₂) có bốn tiếp tuyến chung Δ₁, Δ₂, Δ₃ và Δ₄