Chứng minh rằng trong tam giác ABC ta có các hệ thức: sin A = sinB.cosC + sinC.cosB

Bài 3: Các hệ thức lượng trong tam giác và giải tam giác

Bài 2.35 trang 102 Sách bài tập Hình học 10: Chứng minh rằng trong tam giác ABC ta có các hệ thức:

    a) sin A = sinB.cosC + sinC.cosB

    b) h_a = 2R sinB. sinC

Lời giải:

    a) Theo định lý sin ta có:

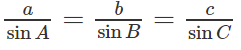
    Do đó: a = 2R.sinA, b = 2R.sinB, c = 2R.sinC

    Thay các giá trị này vào biểu thức: a = b.cosC + c.cosB, ta có:

    2R.sinA = 2R.sinB.cosC + 2R.sinC.cosB

    ⇒ sin A = sinB.cosC + sinC.cosB

    b) Học sinh tự chứng minh.