Cho phương trình x^2 + y2 - 2mx - 4(m - 2)y + 6 - m = 0. Tìm điều kiện của m để (1) là phương trình

Ôn tập chương 3

Bài 3.42 trang 165 Sách bài tập Hình học 10: Cho phương trình x² + y₂ - 2mx - 4(m - 2)y + 6 - m = 0

    a) Tìm điều kiện của m để (1) là phương trình của đường tròn, ta kí hiệu là (C_m).

    b) Tìm tập hợp các tâm của (C_m) khi m thay đổi.

Lời giải:

    a) (1) là phương trình của đường tròn khi và chỉ khi:

    a₂ + b₂ - c = 0

    ⇔ m₂ + 4(m - 2)² - 6 + m > 0

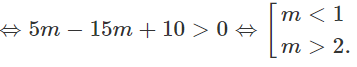
    b) (C_m) có tâm I(x;y) thỏa mãn:

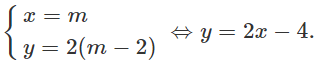
    Vậy tập hợp các tâm của (C_m) là một phần của đường thẳng Δ: y = 2x - 4 thỏa mãn điều kiện giới hạn : x < 1 hay x > 2