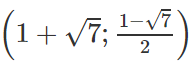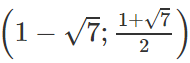Cho elip (E): x^2 + 4y^2> = 16. Xác định tọa độ các tiêu điểm và các đỉnh của elip (E)

Ôn tập chương 3

Bài 3.45 trang 165 Sách bài tập Hình học 10: Cho elip (E): x² + 4y² = 16

    a) Xác định tọa độ các tiêu điểm và các đỉnh của elip (E).

    b) Viết phương trình đường thẳng Δ đi qua điểm M(1; 1/2) và vectơ pháp tuyến n = (1;2)

    c) Tìm tọa độ giao điểm A và B của đường thẳng Δ và elip (E). Chứng minh MA = MB.

Lời giải:

    (E): x² + 4y² = 16

    a)

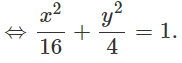
    Ta có: a² = 16, b² = 4

    ⇒ c² = a² - b² = 12

    ⇒ c = 2√3

    Vậy (E) có hai tiêu điểm: F₁(-2√3; 0) và F₂(2√3; 0) và các đỉnh A₁(-4;0), A₂(4;0), B₁(0;-2), B₂(0;2)

    b) Phương trình Δ có dạng : (x - 1) + 2(y - 1/2) = 0 hay x + 2y - 2 = 0

    c) Tọa độ của giao điểm của Δ và (E) là nghiệm của hệ :

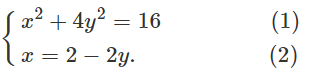
    Thay (2) vào (1) ta được :

    (2 - y)² + 4y² = 16

    ⇔ (1 - y)² + y² = 4

    ⇔ 2y² - 2y - 3 = 0 (3)

    Phương trình (3) có hai nghiệm y_A, y_B thỏa mãn

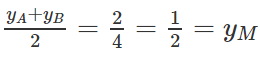
    Vậy MA = MB.

    Ta có:

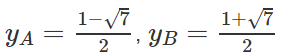
    x_A = 1 + √7, x_BA = 1 - √7

    Vậy A có tọa độ là , B có tọa độ là