Tìm cực trị của các hàm số sau: y = −2x^2 + 7x − 5; y = x^3 − 3x^2 − 24x + 7; y = (x + 2)^2 . (x − 3)^3

Bài 2: Cực trị của hàm số

Giải bài 17 trang 15 SBT Giải tích 12 Bài 2: Cực trị của hàm số giúp học sinh biết cách làm bài tập trong SBT Toán 12.

Bài 1.17 trang 15 Sách bài tập Giải tích 12: Tìm cực trị của các hàm số sau:

a) y = −2x² + 7x − 5

b) y = x³ − 3x² − 24x + 7

c) y = (x + 2)².(x − 3)³

Lời giải:

a) y = −2x² + 7x − 5. TXĐ: R

y′ = −4x + 7, y′ = 0 ⇔ x = 7/4

y′′ = −4 ⇒ y′′(7/4) = −4 < 0

Vậy x = 7/4 là điểm cực đại của hàm số và y_CD = 9/8

b) y = x³ − 3x² − 24x + 7. TXĐ: R

y′ = 3x² − 6x – 24 = 3(x² − 2x − 8)

y′ = 0 ⇔

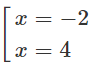
Vì y′′(−2) = −18 < 0, y′′(4) = 18 > 0 nên hàm số đạt cực đại tại x = -2; đạt cực tiểu tại x = 4 và y_CĐ = y(-2) = 35; y_CT = y(4) = -73.

e) TXĐ: R

y′ = 2(x + 2).(x − 3)³ + 3(x + 2)².(x − 3)² = 5x(x + 2).(x − 3)²

y′= 0 ⇔

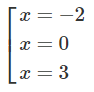
Bảng biến thiên:

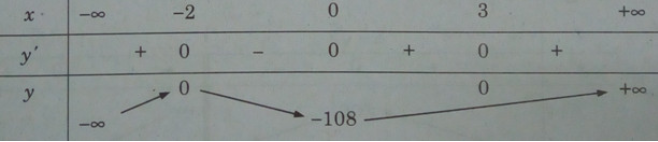
Từ đó suy ra y_CĐ = y(-2) = 0; y_CT = y(0) = -108.