Tìm cực trị của các hàm số sau: y = (x +1) / (x^2 + 8); y = (x^2 - 2x + 3) / (x -1); y = (x^2 + x - 5) / (x + 1)

Bài 2: Cực trị của hàm số

Giải bài 18 trang 15 SBT Giải tích 12 Bài 2: Cực trị của hàm số giúp học sinh biết cách làm bài tập trong SBT Toán 12.

Bài 1.18 trang 15 Sách bài tập Giải tích 12: Tìm cực trị của các hàm số sau:

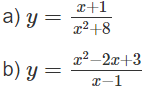
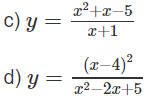
Lời giải:

a) TXĐ : R

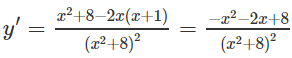
y′= 0 ⇔

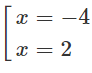
Bảng biến thiên:

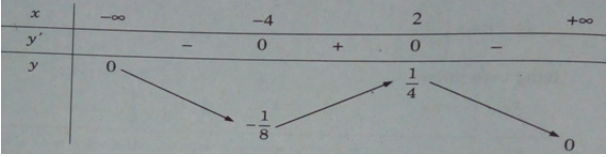
Hàm số đạt cực đại tại x = 2, cực tiểu tại x = -4 và y_CD = y(2) = 1/4; y_CT = y(−4) = −1/8

b) Hàm số xác định và có đạo hàm với mọi x ≠ 1.

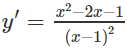
y′=0 ⇔

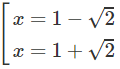
Bảng biến thiên:

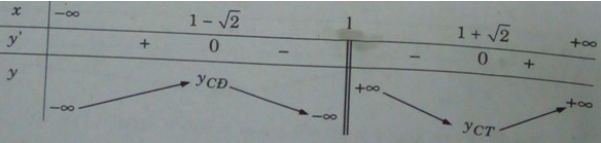
Hàm số đạt cực đại tại x = 1 − √2 và đạt cực tiểu tại x = 1 + √2, ta có:

y_CD = y(1 − √2) = −2√2;

y_CT = y(1 + √2) = 2√2.

c) TXĐ: R\{-1}

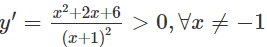
Hàm số đồng biến trên các khoảng và do đó không có cực trị.

d) Vì x² – 2x + 5 luôn luôn dương nên hàm số xác định trên (−∞; +∞)

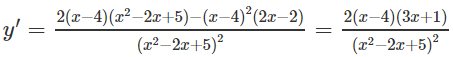
y′ = 0 ⇔

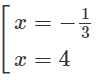
Bảng biến thiên:

Hàm số đạt cực đại tại x = −1/3, đạt cực tiểu tại x = 4 và y_CD = y(−1/3) = 13/4; y_CT = y(4) = 0