Cho đường thẳng và mặt phẳng (α) : 2x – 2y + z + 3 = 0. Chứng minh rằng Δ song song với (α)

Bài 3: Phương trình đường thẳng

Bài 3.37 trang 131 Sách bài tập Hình học 12: Cho đường thẳng:

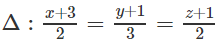
và mặt phẳng (α) : 2x – 2y + z + 3 = 0

a) Chứng minh rằng Δ song song với (α).

b) Tính khoảng cách giữa Δ và (α)

Lời giải:

a) Ta có: a_Δ→ = (2; 3; 2) và n_α→ = (2; −2; 1)

a_Δ→.n_α→ = 4 – 6 + 2 = 0 (1)

Xét điểm M₀(-3; -1; -1) thuộc Δ , ta thấy tọa độ M₀ không thỏa mãn phương trình của (α) . Vậy M₀ ∉ (α) (2).

Từ (1) và (2) ta suy ra Δ // (α).

b) d(α,(α)) = d(M₀,(α))

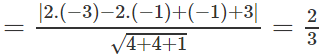
Vậy khoảng cách giữa đường thẳng α và mặt phẳng (α) là 2/3.