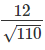Bài 3.38 trang 131 Sách bài tập Hình học 12

Bài 3: Phương trình đường thẳng

Bài 3.38 trang 131 Sách bài tập Hình học 12:

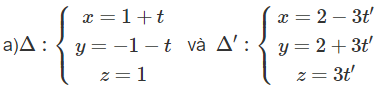
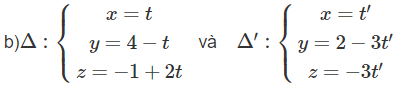
Lời giải:

a) Gọi (α) là mặt phẳng chứa Δ và song song với Δ′. Hai vecto có giá song song hoặc nằm trên (α) là: a→ = (1; −1; 0) và a'→ = (−1; 1; 1). Suy ra n_α→ = (−1; −1; 0)

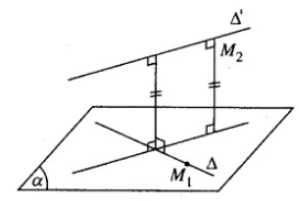
(α) đi qua điểm M₁(1; -1; 1) thuộc Δ và có vecto pháp tuyến: n_α'→ = (1; 1; 0)

Vậy phưong trình của mặt phẳng (α) có dạng x – 1 + y + 1 = 0 hay x + y = 0

Ta có: M₂(2; 2; 0) thuộc đường thẳng Δ′

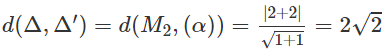
b) Hai đường thẳng Δ và Δ′ có phương trình là:

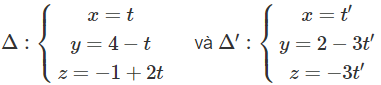
Phương trình mặt phẳng (α) chứa Δ và song song với Δ′ là 9x + 5y – 2z – 22 = 0

Lấy điểm M’(0; 2; 0) trên Δ′ .

Ta có:

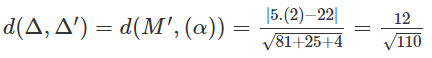
Vậy khoảng cách giữa hai đường thẳng Δ và Δ′ là