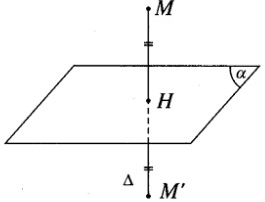
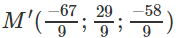Cho điểm M(1; -1; 2) và mặt phẳng (α): 2x – y + 2z + 12 = 0. Tìm tọa độ điểm H là hình chiếu vuông góc

Bài 3: Phương trình đường thẳng

Bài 3.41 trang 132 Sách bài tập Hình học 12: Cho điểm M(1; -1; 2) và mặt phẳng (α): 2x – y + 2z + 12 = 0

a) Tìm tọa độ điểm H là hình chiếu vuông góc của điểm M trên mặt phẳng (α) ;

b) Tìm tọa độ điểm M’ đối xứng với M qua mặt phẳng (α) .

Lời giải:

a) Phương trình tham số của đường thẳng Δ đi qua điểm M(1; -1; 2) và vuông góc với mặt phẳng (α): 2x – y + 2z + 12 = 0 là:

Δ

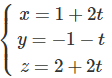
Xét điểm H(1 + 2t; -1 – t; 2 + 2t) ∈ Δ

Ta có H ∈ (α) ⇔ 2(1 + 2t) + (1 + t) + 2(2 + 2t) + 12 = 0 ⇔ t = −19/9

Vậy ta được

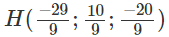
b) H là trung điểm của MM’, suy ra x_M′ = 2x_H – x_M = −67/9

y_M′ = 2y_H – y_M = 29/9

z_M′ = 2z_H – z_M = −58/9

Vậy ta được