Tìm các giá trị của m để phương trình : x^3 – 3x^2 – m = 0 có ba nghiệm phân biệt

Bài 3: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

Giải bài 37 trang 21 SBT Giải tích 12 Bài 3: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số giúp học sinh biết cách làm bài tập trong SBT Toán 12.

Bài 1.37 trang 21 Sách bài tập Giải tích 12: Tìm các giá trị của m để phương trình : x³ – 3x² – m = 0 có ba nghiệm phân biệt.

Lời giải:

Đặt f(x) = x³ – 3x² (C₁)

y = m (C₂)

Phương trình x³ – 3x² – m = 0 có ba nghiệm phân biệt khi và chỉ khi (C₁) và (C₂) có ba giao điểm.

Ta có:

f′(x) = 3x² − 6x = 3x(x − 2) = 0

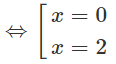
Bảng biến thiên:

Suy ra (C₁), (C₂) cắt nhau tại 3 điểm khi -4 < m < 0

Kết luận : Phương trình x³ – 3x² – m = 0 có ba nghiệm phân biệt với những giá trị của m thỏa mãn điều kiện: -4 < m < 0.