Bài tập trắc nghiệm trang 21, 22 Sách bài tập Giải tích 12

---

Bài 3: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số

Giải bài tập trắc nghiệm trang 21, 22 SBT Giải tích 12 Bài 3: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số giúp học sinh biết cách làm bài tập trong SBT Toán 12.

Bài tập trắc nghiệm trang 21, 22 Sách bài tập Giải tích 12:

Bài 1.41: Giá trị lớn nhất của hàm số y = -x² + 4x - 5 trên đoạn [0;3] bằng:

A. -1              B. 1

C. 2              D. 0

Bài 1.42: Giá trị nhỏ nhất của hàm số f(x) = x³ + 3x² - 9x - 7 trên đoạn [-4;3] bằng:

A. -5              B. 0

C. 7              D. -12

Bài 1.43: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số sau trên đoạn [0;2] bằng

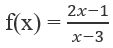
A. 1/3 và -3              B. 3/2 và -1

C. 2 và -3              D. 1/2 và 5

Bài 1.44: Tìm hai số có hiệu là 13 sao cho tích của chúng là bé nhất

A. 13 và 0              B. 13/2 và -13/2

C. 15 và 2              D. 30 và 15

Bài 1.45: Giá trị lớn nhất của hàm số sau trên khoảng (-∞; +∞) là:

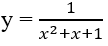
A. 1              B. 4/3

C. 5/3              D. 0

Bài 1.46: Giá trị nhỏ nhất của hàm số sau trên khoảng (0; π/2) là:

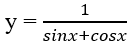
A. 1              B. 2√2

C. -√2              D. 2√/2

Lời giải:

Đáp án và hướng dẫn giải

Bài	1.41	1.42	1.43	1.44	1.45	1.46
Đáp án	A	D	A	B	B	D

Bài 1.41: Đáp án: A.

Ta có y(0) = -5, y(3) = -2, tọa độ đỉnh: x = -b/2a = 2

⇒ y(2) = -4 + 8 - 5 = -1; max y = max(-5; -2; -1) = -1.

Cách khác: Vì a = -1 nên parabol y = -x² + 4x - 5 đạt cực đạt tại đỉnh (2; -1). Vì vậy giá trị lớn nhất của hàm số trên đoạn [0;3] là y(2) = -1.

Bài 1.42: Đáp án: D.

Ta có f(x) = x³ + 3x² - 9x - 7 ⇒ f'(x) = 3x² + 6x - 9 = 0

⇔

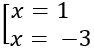
f(-4) = 13, f(-3) = 30, f(1) = -12, f(3) = 20

Vậy min f(x) = -12.

Bài 1.43: Đáp án: A.

Tập xác định: D = R \{3}

∀x ∈ D.

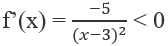
Do đó f(x) nghịch biến trên (-∞; 3) và (3; +∞).

Ta thấy [0;2] ⊂ (-∞;3). Vì vậy

max f(x) = f(0) = 1/3, min f(x) = f(2) = -3.

Bài 1.44: Đáp án: B.

Gọi một trong hai số phải tìm là x, ta có số kia là x + 13

Xét tích p(x) = x(x + 13) = x² + 13x;

p'(x) = 2x + 13; p'(x) = 0 ⇔ x = -13/2.

Bảng biến thiên

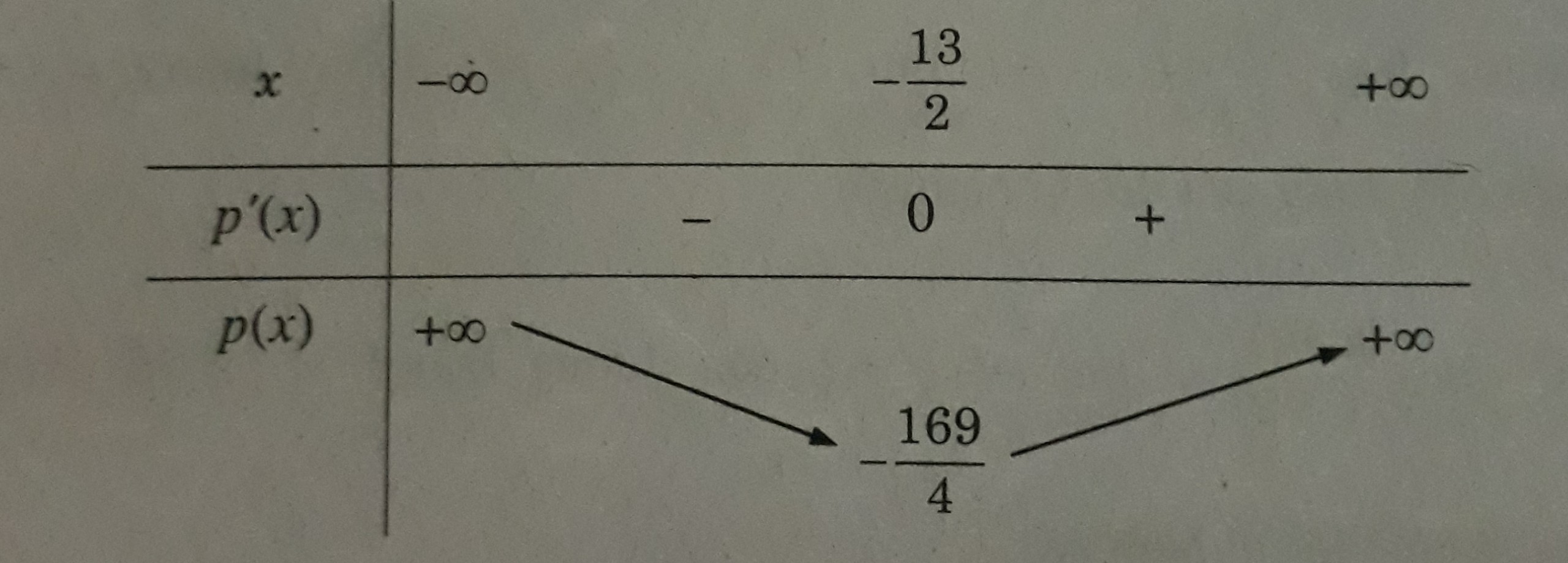
Vậy tích hai số là bé nhất khi một số là x = -13/2 và số kia là x + 13 = 13/2.

Bài 1.45: Đáp án: B.

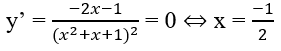
Bảng biến thiên

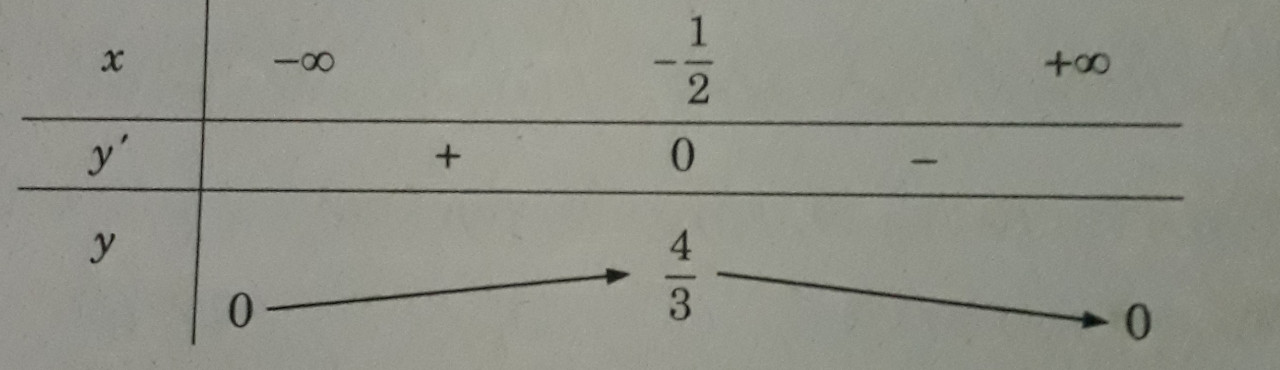
max y = 4/3.

Bài 1.46: Đáp án: D.

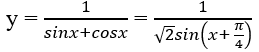
Trên khoảng (0; π/2), sin(x + π/4) ≤ 1;

Dấu "=" xảy ra ⇔ x = π/4

Suy ra giá trị nhỏ nhất của hàm số là min y = y(π/4) = √2/2.