Xét sự đồng biến, nghịch biến của các hàm số: y = x − sinx, x ∈ [0; 2π]; y = sin(1/x), (x > 0)

Bài 1: Sự đồng biến, nghịch biến của hàm số

Giải bài 4 trang 8 SBT Giải tích 12 Bài 1: Sự đồng biến, nghịch biến của hàm số giúp học sinh biết cách làm bài tập trong SBT Toán 12.

Bài 1.4 trang 8 Sách bài tập Giải tích 12: Xét sự đồng biến, nghịch biến của các hàm số:

a) y = x − sinx, x ∈ [0; 2π].

c) y = sin(1/x), (x > 0)

Lời giải:

a) y = x – sinx, x ∈ [0; 2π].

y′ = 1 – cosx ≥ 0 với mọi x ∈ [0; 2π]

Dấu “=” xảy ra chỉ tại x = 0 và x = 2π.

Vậy hàm số đồng biến trên đoạn [0; 2π].

c) Xét hàm số y = sin(1/x) với x > 0.

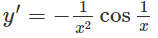
Giải bất phương trình sau trên khoảng (0; +∞):

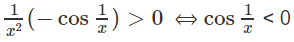
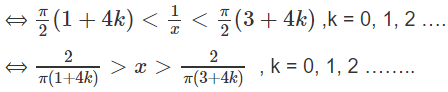
Do đó, hàm số đồng biến trên các khoảng

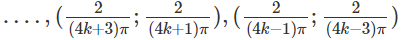
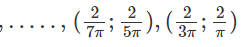
Và nghịch biến trên các khoảng

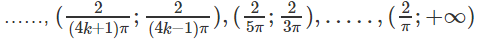
với k = 0, 1, 2 …