Chứng minh các bất đẳng thức sau: tanx > sinx, 0 < x < π/2. Bài 1.7 trang 8 Sách bài tập Giải tích 12

Bài 1: Sự đồng biến, nghịch biến của hàm số

Giải bài 7 trang 8 SBT Giải tích 12 Bài 1: Sự đồng biến, nghịch biến của hàm số giúp học sinh biết cách làm bài tập trong SBT Toán 12.

Bài 1.7 trang 8 Sách bài tập Giải tích 12: Chứng minh các bất đẳng thức sau:

a) tanx > sinx, 0 < x < π/2

b)

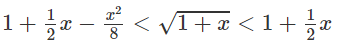
với 0 < x < +∞

Lời giải:

a) Xét hàm số f(x) = tanx − sinx trên nửa khoảng [0; π/2);

x ∈ [0;1/2)

Dấu “=” xảy ra khi x = 0.

Suy ra f(x) đồng biến trên nửa khoảng [0; π/2)

Mặt khác, ta có f(0) = 0, nên f(x) = tanx – sinx > 0 hay tanx > sinx với mọi x ∈ [0; 1/2)

b) Xét hàm số h(x) trên [0; +∞)

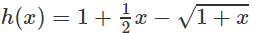
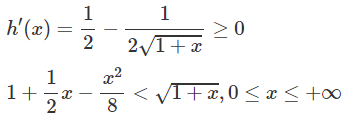
Dấu “=” xẩy ra chỉ tại x = 0 nên h(x) đồng biến trên nửa khoảng [0; +∞).

Vì h(x) = 0 nên

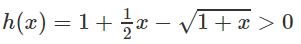
Hay

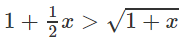
Xét hàm số trên f(x) trên [0; +∞);

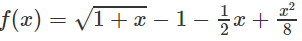
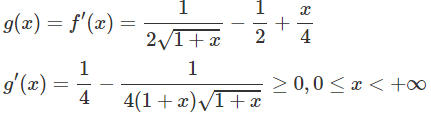
Vì g(0) = 0 và g(x) đồng biến trên nửa khoảng [0; +∞) nên g(x) ≥ 0, tức là f′(x) ≥ 0 trên khoảng đó và vì dấu “=” xảy ra chỉ tại x = 0 nên f(x) đồng biến trên nửa khoảng .

Mặt khác, ta có f(0) = 0 nên

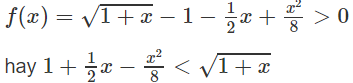
Với mọi 0 < x < +∞.