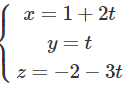Cho mặt phẳng (α) : 2x + y + z – 1 = 0 và đường thẳng d: (x - 1)/2 = y/1 = (z + 2)/-3. Gọi M là giao điểm

Bài 3: Phương trình đường thẳng

Bài 3.44 trang 132 Sách bài tập Hình học 12: Cho mặt phẳng (α) : 2x + y + z – 1 = 0

và đường thẳng

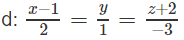
Gọi M là giao điểm của d và (α), hãy viết phương trình của đường thẳng Δ đi qua M vuông góc với d và nằm trong (α)

Lời giải:

Xét phương trình:

2(1 + 2t) + (t) + (−2 – 3t) – 1 = 0 ⇔ 2t – 1= 0 ⇔ t = 1/2

Vậy đường thẳng d cắt mặt phẳng (α) tại điểm M(2; 1/2; −7/2).

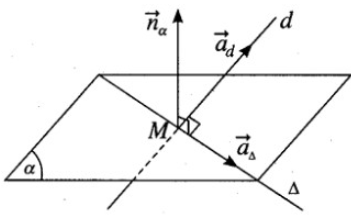
Ta có vecto pháp tuyến của mặt phẳng (α) và vecto chỉ phương của đường thẳng d lần lượt là n_α→ = (2; 1; 1) và a_d→ = (2; 1; −3).

Gọi a_Δ→ là vecto pháp tuyến của Δ, ta có a_Δ→ ⊥ n_α→ và a_Δ→ ⊥ a_d→.

Suy ra a_Δ→ = n_α→ ∧ n_d→ = (−4; 8; 0) hay a_Δ→ = (1; −2; 0)

Vậy phương trình tham số của Δ là