Chứng minh rằng d1 và d2 cùng nằm trong một mặt phẳng (α). Viết phương trình của (α)

Bài 3: Phương trình đường thẳng

Bài 3.45 trang 132 Sách bài tập Hình học 12:

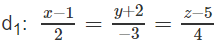
và

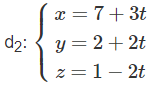
a) Chứng minh rằng d₁ và d₂ cùng nằm trong một mặt phẳng (α).

b) Viết phương trình của (α).

Lời giải:

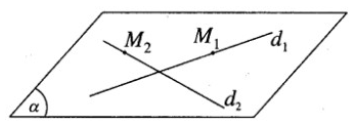
a) Ta có ad₁→ = (2; −3; 4) và ad₂→ = (3; 2; −2)

n→ = ad₁→ ∧ ad₂→ = (−2; 16; 13)

Lấy điểm M₁(1; -2; 5) trên d₁ và điểm M₂(7; 2; 1) trên d₂.

Ta có M₁M₂→ = (6; 4; −4)

n→. M₁M₂→ = −12 + 64 – 52 = 0

Suy ra d₁ và d₂ cùng nằm trong mặt phẳng (α)

b) Mặt phẳng (α) chứa M₁ và có vecto pháp tuyến là n→, vậy phương trình của (α) là:

–2(x – 1) + 16(y + 2) + 13(z – 5) = 0 – 2(x – 1) + 16(y + 2) + 13(z – 5) = 0 hay 2x – 16y – 13z + 31 = 0