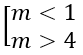Khẳng định nào sau đây đúng. Bài tập trắc nghiệm trang 8, 9 Sách bài tập Giải tích 12

---

Bài 1: Sự đồng biến, nghịch biến của hàm số

Giải bài tập trắc nghiệm trang 8,9 SBT Giải tích 12 Bài 1: Sự đồng biến, nghịch biến của hàm số giúp học sinh biết cách làm bài tập trong SBT Toán 12.

Bài tập trắc nghiệm trang 8, 9 Sách bài tập Giải tích 12:

Bài 1.9: Khẳng định nào sau đây đúng?

A. y = sin3x là hàm số chẵn

B. Hàm số xác định trên R

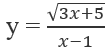
C. Hàm số y = x³ + 4x - 5 đồng biến trên R

D. Hàm số y = sinx + 3x - 1 nghịch biến trên R

Bài 1.10: Hàm số nghịch biến trên khoảng:

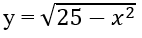
A. (-∞; 0)              B. (-5; 0)

C. (0; 5)              D. (5; +∞)

Bài 1.11: Hàm số đồng biến trên khoảng:

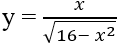
A. (4; +∞)              B. (-4; 4)

C. (-∞; -4)              D. R

Bài 1.12: Phương trình nào sau đây có nghiệm duy nhất trên R?

A. 3sin²x - cos²x + 5 = 0              B. x² + 5x + 6 = 0

C. x⁵ + x³ - 7 = 0              D. 3tanx - 4 = 0

Bài 1.13: Phương trình nào sau đây có nghiệm duy nhất trên R?

A. x² - 7x + 12 = 0              B. x³ + 5x + 6 = 0

C. x⁴ - 3x² + 1 = 0              D. 2sinx.cos²x - 2sinx - cos²x + 1 = 0

Bài 1.14: Phương trình nào sau đây có nghiệm duy nhất trên R?

A. (x - 5)(x² - x - 12) = 0              B. -x³ + x² - 3x + 2 = 0

C. sin²x - 5sinx + 4 = 0              D. sinx - cosx + 1 = 0

Bài 1.15: Tìm giá trị của tham số m để các hàm số y = x³ - 2mx² + 12x - 7 đồng biến trên R.

A. m = 4              B. m ∈ (0; ∞)

C. m ∈ (-∞; 0)              D. -3 ≤ m ≤ 3

Bài 1.16: Tìm giá trị của tham số m để hàm số y nghịch biến trên từng khoảng xác định

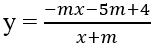
A. m < 1 hoặc m > 4              B. 0 < m < 1

C. m > 4              D. 1 ≤ m ≤ 4

Lời giải:

Đáp án và hướng dẫn giải

Bài	1.9	1.10	1.11	1.12	1.13	1.14	1.15	1.16
Đáp án	C	C	B	C	B	B	D	A

Bài 1.9: Đáp án: C.

Vì y' = 3x² + 4 > 0, ∀x ∈ R.

Bài 1.10: Đáp án: C.

Gợi ý: Loại A, D vì tập xác định của hàm số là 25 - x² ≥ 0 ⇔ -5 ≤ x ≤ 5.

Loại B, vì

x	-5	0
y	0	5

Bài 1.11: Đáp án: B.

Vì

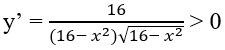
trên tập xác định (-4;4)

Cách khác: Loại A, C, D vì tập xác định của hàm số là (-4;4)

Bài 1.12: Đáp án: C

Vì f'(x) = (x⁵ + x³ - 7)' = 5x⁴ + 3x² ≥ 0, ∀x ∈ R (dấu "=" xảy ra ⇔ x = 0). Suy ra f(x) đồng biến trên R. Mặt khác f(0) = -7, f(2) = 32 + 8 - 7 = 33 > 0. Hàm f(x) liên tục trên đoạn [0;2] nên tồn tại x₀ ∈ (0;2) để f(x₀) = 0. Suy ra f(x) = 0 có nghiệm duy nhất trên R.

Cách khác: Phương trình 3sin²x - cos²x + 5 = 0

⇔ 3sin²x + sin²x + 4 = 4(sin²x + 1) = 0, vô nghiệm

Các phương trình x² - 5x + 6 = 0 và 3tanx - 4 = 0 có nhiều hơn một nghiệm. Từ đó suy ra phương trình x⁵ + x³ - 7 = 0 có nghiệm duy nhất trên R.

Bài 1.13: Đáp án:B.

Với f(x) = x³ + 5x + 6 thì vì f'(x) = 3x² + 5 > 0, ∀x ∈ R nên hàm số f(x) luôn đồng biến trên R. Mặt khác f(-1) = 0. Vậy phương trình f(x) = 0 có nghiệm duy nhất trên R.

Bài 1.14: Đáp án: B.

Các phương trình còn lại có nhiều hơn một nghiệm:

(x - 5)(x² - x - 12) = 0 có các nghiệm x = 5, 4, -3.

sin²x - 5sinx + 4 = 0 ⇔ sinx = 1, có vô số nghiệm

sinx - cosx + 1 = 0 có các nghiệm x = 0, x = 3π/2.

Bài 1.15: Đáp án: D.

Hàm số đồng biến trên tập xác định R khi và chỉ khi

y' = 3x² - 4mx + 12 ≥ 0, ∀x ⇔ Δ' = 4m² - 36 ≤ 0 ⇔ -3 ≤ m ≤ 3.

Bài 1.16: Đáp án: A.

Hàm số nghịch biến trên từng khoảng (-∞; -m), (-m; +∞) khi và chỉ khi

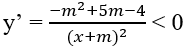
⇔ -m² + 5m - 4 < 0

⇔