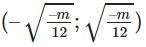Cho hàm số: y = 4x^3 + mx (m là tham số) (1). Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số ứng với m = 1

Bài tập ôn tập chương 1

Giải bài 75 trang 39 SBT Giải tích 12 Bài tập ôn tập chương 1 giúp học sinh biết cách làm bài tập trong SBT Toán 12.

Bài 1.75 trang 39 Sách bài tập Giải tích 12: Cho hàm số: y = 4x³ + mx (m là tham số) (1)

a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số ứng với m = 1.

b) Viết phương trình tiếp tuyến của (C) song song với đường thẳng y = 13x + 1.

c) Xét sự biến thiên của hàm số (1) tùy thuộc vào giá trị m.

Lời giải:

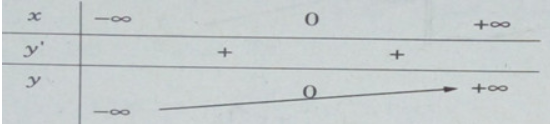
a) y = 4x³ + x, y′ = 12x² + 1 > 0, ∀ x ∈ R

Bảng biến thiên:

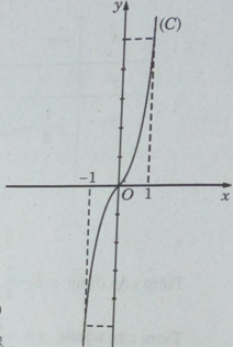
Đồ thị:

b) Giả sử tiếp điểm cần tìm có tọa độ (x₀; y₀) thì f′(x₀) = 12x²₀ + 1 = 13 (vì tiếp tuyến song song với đường thẳng (d): y = 3x + 1). Từ đó ta có: x₀ = 1 hoặc x₀ = -1

Vậy có hai tiếp tuyến phải tìm là y = 13x + 8 hoặc y = 13x - 8

c) Vì y’ = 12x² + m nên m ≥ 0; y” = –6(m² + 5m)x + 12m

    +) Với m ≥ 0 ta có y’ > 0 (khi m = 0; y’ = 0 tại x = 0).

Vậy hàm số (1) luôn luôn đồng biến khi m ≥ 0; y” = –6(m² + 5m)x + 12m

    +) Với m < 0 thì y = 0 ⇔

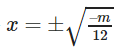
Từ đó suy ra:

y’ > 0 với

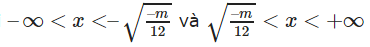
y’ < 0 với

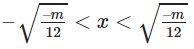
Vậy hàm số (1) đồng biến trên các khoảng

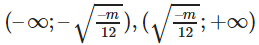
và nghịch biến trên khoảng