Cho hàm số. Xác định a để hàm số luôn đồng biến. Xác định a để đồ thị của hàm số cắt trục hoành

Bài tập ôn tập chương 1

Giải bài 77 trang 40 SBT Giải tích 12 Bài tập ôn tập chương 1 giúp học sinh biết cách làm bài tập trong SBT Toán 12.

Bài 1.77 trang 40 Sách bài tập Giải tích 12: Cho hàm số

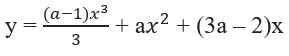
a) Xác định a để hàm số luôn đồng biến.

b) Xác định a để đồ thị của hàm số cắt trục hoành tại ba điểm phân biệt.

c) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số ứng với a = 3/2.

Từ đó suy ra đồ thị của hàm số

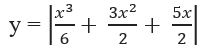
Lời giải:

a) Ta có

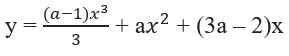
y' = (a - 1)x² + 2ax + 3a - 2.

Với a = 1, y' = 2x + 1 đổi dấu khi x đi qua -1/2. Hàm số không đồng biến.

Với a ≠ 1 thì với mọi x mà tại đó y' ≥ 0

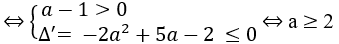
(y' = 0 chỉ tại x = -2, khi a = 2).

Vậy với a ≥ 2 hàm số luôn đồng biến

b) Đồ thị cắt trục hoành tại ba điểm phân biệt khi và chỉ khi phương trình y = 0 có ba nghiệm phân biệt. Ta có

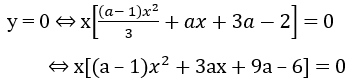
y = 0 có ba nghiệm phân biệt khi và chỉ khi phương trình

(a - 1)x² + 3ax + 9a - 6 = 0

Có hai nghiệm phân biệt khác 0. Muốn vậy, ta phải có

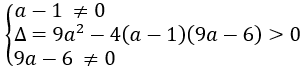
Giải hệ trên, ta được:

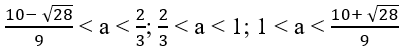
c) Khi a = 3/2 thì

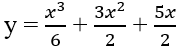
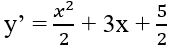
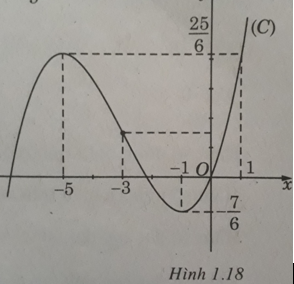
y' = 0 ⇔ x² + 6x + 5 = 0 ⇔ x = -1 hoặc x = -5.

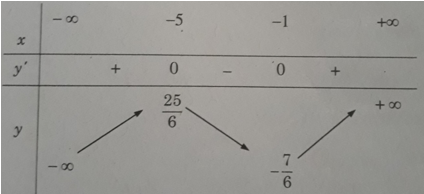
Đồ thị như trên Hình 1.18

Vì

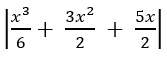
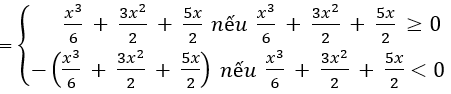
nên từ đồ thị (C) ta suy ngay ra đồ thị của hàm số

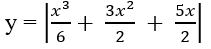
như trên Hình 1.19