Cho hàm số : y = x^3 – 3x^2. Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho

Bài tập ôn tập chương 1

Giải bài 78 trang 40 SBT Giải tích 12 Bài tập ôn tập chương 1 giúp học sinh biết cách làm bài tập trong SBT Toán 12.

Bài 1.78 trang 40 Sách bài tập Giải tích 12: Cho hàm số : y = x³ – 3x²

a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho.

b) Tìm các giá trị của tham số m để phương trình: x³ – 3x² – m = 0 có ba nghiệm phân biệt.

(Đề thi tốt nghiệp THPT năm 2008).

Lời giải:

a) TXĐ: D = R

Sự biến thiên:

y′ = 3x² – 6x = 3x(x – 2)

y′=0 ⇔

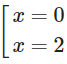
Hàm số đồng biến trên mỗi khoảng (–∞;0), (2;+∞)

Hàm số nghịch biến trên khoảng (0; 2).

Hàm số đạt cực đại tại x = 0 ; y_CĐ = y(0) = 0

Hàm số đạt cực tiểu tại x = 2; y_CT = y(2) = -4.

Giới hạn:

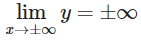
Điểm uốn: y” = 6x – 6, y” = 0 ⇔ x = 1; y(1) = –2

Suy ra đồ thị có điểm uốn I(1; -2)

Bảng biến thiên:

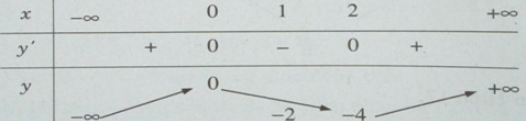
Đồ thị:

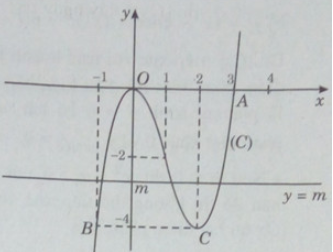
Đồ thị cắt trục hoành tại O(0;0), A(3;0). Đồ thị đi qua điểm B(-1;-4); C(2;-4).

b) x³ – 3x² – m = 0 ⇔ x³ – 3x² = mx³ – 3x² – m = 0 ⇔ x³ – 3x² = m (∗)

Phương trình (∗) có 3 nghiệm phân biệt khi và chỉ khi đường thẳng y = m cắt (C) tại 3 điểm phân biệt. Từ đó suy ra: – 4 < m < 0.