Bài tập trắc nghiệm trang 41, 42, 43 Sách bài tập Giải tích 12

---

Bài tập ôn tập chương 1

Giải bài tập trắc nghiệm trang 41, 42, 43 SBT Giải tích 12 Bài tập ôn tập chương 1 giúp học sinh biết cách làm bài tập trong SBT Toán 12.

Bài tập trắc nghiệm trang 41, 42, 43 Sách bài tập Giải tích 12:

Bài 1.84: Hàm số đồng biến trên khoảng:

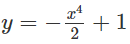
A. (-∞; 0);              B. (1; +∞);

C. (-3; 4);              D. (-∞; 1).

Bài 1.85: Xác định giá trị của tham số m để hàm số

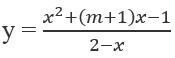
nghịch biến trên mỗi khoảng xác định của nó

A. m = −1;              B. m > 1;

C. m ∈ (−1;1);              D. m ≤ −5/2.

Bài 1.86: Hoành độ các điểm cực tiểu của hàm số y = x⁴ + 3x² + 2 là:

A. x = −1;              B. x = 5;

C. x = 0;              D. x = 1, x = 2.

Bài 1.87: Giá trị lớn nhất của hàm số sau là:

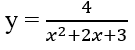
A. 3;              B. 2;

C. -5;              D. 10.

Bài 1.88: Cho hàm số:

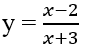
Khẳng định nào sau đây là đúng?

A. Hàm số đồng biến trên từng khoảng xác định;

B. Hàm số đồng biến trên khoảng (-∞;+∞);

C. Hàm số nghịch biến trên từng khoảng xác định;

D. Hàm số nghịch biến trên khoảng (-∞;+∞).

Bài 1.89: Tọa độ giao điểm của đồ thị các hàm số:

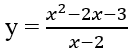
và y = x + 1 là:

A. (2; 2);              B. (2; -3);

C(-1; 0);              D. (3; 1).

Bài 1.90: Số giao điểm của đồ thị hàm số y = (x − 3)(x² + x + 4) với trục hoành là:

A. 2;              B. 3;

C. 0;              D. 1.

Bài 1.91: Xác định giá trị của tham số m để hàm số y = x³ + mx² - 3 có cực đại và cực tiểu.

A. m = 3;              B. m > 0;

C. m ≠ 0;              D. m < 0.

Bài 1.92: Xác định giá trị của tham số m để phương trình 2x³ + 3mx² - 5 = 0 có nghiệm duy nhất.

Bài 1.93: Tìm khẳng định đúng trong các khẳng định sau đây:

A. Hàm số y = x³ - 5 có hai cực trị;

B. Hàm số y = x⁴/4 + 3x² - 5 luôn đồng biến;

C. Tiệm cận ngang của đồ thị hàm số là y = -3;

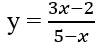
D. Đồ thị hàm số sau có hai tiệm cận đứng

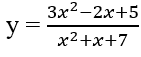
Bài 1.94: Tìm khẳng định sai trong các khẳng định sau đây:

A. Hàm số y = 4cosx - 5sin²x - 3 là hàm số chẵn;

B. Đồ thị hàm số sau có hai tiệm cận đứng

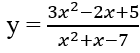
C. Hàm số luôn nghịch biến;

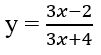
D. Hàm số

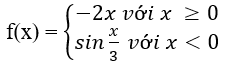
không có đạo hàm tại x = 0.

Bài 1.95: Xác định giá trị của tham số m để phương trình x³ + mx² + x - 5 = 0 có nghiệm dương

A. m = 5;              B. m ∈ R;

C. m = -3;              D. m < 0

Bài 1.96: Xác định giá trị của tham số m để phương trình

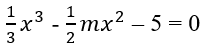
có nghiệm duy nhất

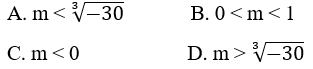
Lời giải:

Đáp án và hướng dẫn giải

Bài	1.84	1.85	1.86	1.87	1.88	1.89	1.90
Đáp án	A	D	C	B	A	C	D
Bài	1.91	1.92	1.93	1.94	1.95	1.96
Đáp án	C	B	C	C	B	D

Bài 1.84: Đáp án: A.

Hàm số dạng này có một điểm cực đại tại x = 0. Vậy hàm số đồng biến trên khoảng (-∞; 0).

Bài 1.85: Đáp án: D.

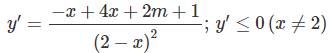
⇔ Δ′ = 2m + 5 ≤ 0

dấu “=” xảy ra nhiều nhất tại hai điểm, nên hàm số nghịch biến trên các khoảng (-∞; 2)

và (2; +∞) khi m ≤ −5/2.

Bài 1.86: Đáp án: C

Ta có y(0) = 2, y(a) = a⁴ + 3ax² + 2 > 2 với mọi a ≠ 0.

Vậy hàm số có một điểm cực tiểu là x = 0.

Bài 1.87: Đáp án: B.

Với mọi x ta đều có

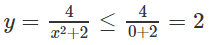
nên hàm số đạt giá trị lớn nhất khi x = -1 hay max y = 2

Bài 1.88: Đáp án: A.

Bài 1.89: Đáp án: C.

Hàm số

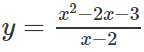
không xác định tại x = 2 nên phải loại (A), (B).

Thay x = 3 vào hàm số trên, ta được y(3) = 0. Mặt khác, hàm số thứ hai có giá trị là 4 khi x = 3, do đó loại (D). Vậy (C) là khẳng định đúng.

Bài 1.90: Đáp án: D.

Vì x² + x + 4 > 0 với mọi x nên phương trình (x − 3)(x² + x + 4) = 0 chỉ có một nghiệm là x = 3. Do đó, đồ thị của hàm số đã cho chỉ có một giao điểm với trục hoành.

Bài 1.91: Đáp án: C.

Để có cực đại, cực tiểu, phương trình y' = 3x² + 2mx = 0 phải có hai nghiệm phân biệt.

Phương trình y' = x(3x + 2m) = 0 có hai nghiệm phân biệt x₁ = 0, x₂ = -2m/3 khi và chỉ khi x ≠ 0.

Bài 1.92: Đáp án: B.

Với m = 0, phương trình 2x³ - 5 = 0 có nghiệm duy nhất.

Với m ≠ 0, đồ thị hàm số y = 2x³ + 3mx² - 5 chỉ cắt Ox tại một điểm khi y_CĐ.y_CT > 0. Ta có y' = 6x² + 6mx = 6x(x + m) = 0 có hai nghiệm là x = 0, x = -m; y(0) = -5, y(-m) = -2m³ + 3m³ - 5 = m³ - 5.

Suy ra y(0).y(-m) = -5(m³ - 5) > 0 ⇔ m <

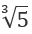
Bài 1.93: Đáp án: C.

y = -3 là tiệm cận ngang của đồ thị hàm số

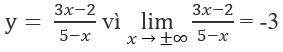
Bài 1.94: Đáp án: B.

Xét f(x) = x³ + mx² + x - 5

Vì

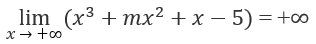
và f(0) = -5 với mọi m ∈ R cho nên phương trình f(x) = 0 luôn có nghiệm dương.

Bài 1.96: Đáp án: D.

Xét hàm số

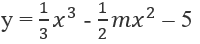
Ta có: y' = x² - mx = 0 ⇔ x = 0 hoặc x = 3

Nếu m = 0: Phương trình thành x³/3 - 5 = 0, có nghiệm duy nhất.

Nếu m ≠ 0: Phương trình đã cho có nghiệm duy nhất khi và chỉ khi cực đại và cực tiểu của hàm số

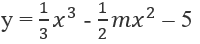
cùng dấu.