Cho hàm số: y = f(x) = x^4 – 2mx^2 + m^3 – m^2. Khảo sát sự biến thiên và vẽ đồ thị của hàm số khi m = 1

Bài tập ôn tập chương 1

Giải bài 80 trang 40 SBT Giải tích 12 Bài tập ôn tập chương 1 giúp học sinh biết cách làm bài tập trong SBT Toán 12.

Bài 1.80 trang 40 Sách bài tập Giải tích 12: Cho hàm số: y = f(x) = x⁴ – 2mx² + m³ – m²

a) Khảo sát sự biến thiên và vẽ đồ thị của hàm số khi m = 1.

b) Xác định m để đồ thị (C_m) của hàm số đã cho tiếp xúc với trục hoành tại hai điểm phân biệt.

Lời giải:

a) y = x⁴ – 2x²

y′ = 4x³ – 4x = 4x(x² – 1)

y′ = 0 ⇔

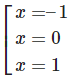
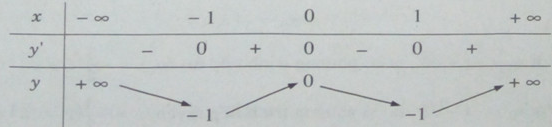
Bảng biến thiên:

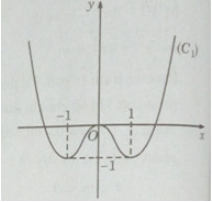
Đồ thị

b) y′ = 4x³ – 4mx = 4x(x² – m)

Để (C_m) tiếp xúc với trục hoành tại hai điểm phân biệt thì điều kiện cần và đủ là phương trình y’ = 0 có hai nghiệm phân biệt khác 0 và y_CT = 0.

    +) Nếu m ≤ 0 thì x² – m ≥ 0 với mọi x nên đồ thị không thể tiếp xúc với trục Ox tại hai điểm phân biệt.

    +) Nếu m > 0 thì y’ = 0 khi x = 0; x = √m hoặc x = -√m.

f(√m) = 0 ⇔ m² – 2m² + m³ – m² = 0 ⇔ m²(m – 2) = 0 ⇔ m = 2 (do m > 0)

Vậy m = 2 là giá trị cần tìm.