Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số y = (x + 2) / (x - 3). Chứng minh rằng giao điểm I
Bài tập ôn tập chương 1
Giải bài 82 trang 41 SBT Giải tích 12 Bài tập ôn tập chương 1 giúp học sinh biết cách làm bài tập trong SBT Toán 12.
Bài 1.82 trang 41 Sách bài tập Giải tích 12: a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
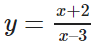
b) Chứng minh rằng giao điểm I của hai tiệm cận của (C) là tâm đối xứng của (C).
c) Tìm điểm M trên đồ thị của hàm số sao cho khoảng cách từ M đến tiệm cận đứng bằng khoảng cách từ M đến tiệm cận ngang.
Lời giải:
a) Học sinh tự làm.
b) Tiệm cận đứng là đường thẳng x = 3.
Tiệm cận ngang là đường thẳng y = 1.
Do đó, giao điểm của hai đường tiệm cận là I(3; 1). Thực hiện phép biến đổi:
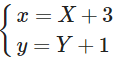
Ta được
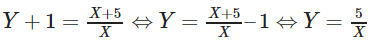
Vì Y = 5/X là hàm số lẻ nên đồ thị (C) của hàm số này có tâm đối xứng là gốc tọa độ I của hệ tọa độ IXY.
c) Giả sử M(x0; y0) ∈ (C). Gọi d1 là khoảng cách từ M đến tiệm cận đứng và d2 là khoảng cách từ M đến tiệm cận ngang, ta có:
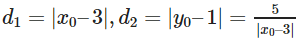
Có hai điểm thỏa mãn đầu bài, đó là hai điểm có hoành độ x0 = 3 + √5 hoặc x0 = 3 - √5

