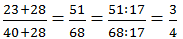Bài 39, 40 trang 12 SBT Toán 6 tập 2
Bài 39, 40 trang 12 SBT Toán 6 tập 2
Bài 39 trang 12 sách bài tập Toán 6 Tập 2: Chứng tỏ rằng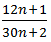 
là phân số tối giản (n ∈ N)
Lời giải:
Vì n ∈ N nên ta phải chứng minh tử và mẫu của phân số có ước chung lớn nhất bằng 1.
Gọi ước chung lớn nhất của 12n + 1 và 30n + 2 là a. Ta chứng minh a = 1
Ta có: (12n + 1) ⋮ a nên 5(12n + 1) ⋮ a
(30n + 2) ⋮ a nên 2(30n + 2) ⋮ a
Suy ra: [5(12n + 1) – 2(30n + 2)] ⋮ a
⇔(60 n + 5 – 60n - 4) ⋮ a
⇔1 ⋮ a ⇔ a = 1
Vậy 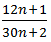là phân số tối giản (n ∈ N)
Bài 40 trang 12 sách bài tập Toán 6 Tập 2: Cộng cả tử và mẫu của phân số 23/40 với cùng một số tự nhiên n rồi rút gọn, ta được phân số 3/4 . Tìm số n
Lời giải:
Theo đề bài, ta có: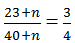 
(n ∈ N)
⇔ 4(23 + n) = 3 (40 + n) ⇔ 4n + 92 = 120 + 3n
⇔ 4n – 3n = 120 – 92 ⇔n = 28
Vậy n = 28.
Thử lại: 
