Bài II.1, II.2, II.3 trang 154 SBT Toán 7 tập 1

Bài II.1, II.2, II.3 trang 154 SBT Toán 7 tập 1

Bài II.1: Trên hình bs 6 , có bao nhiêu cặp tam giác bằng nhau ?

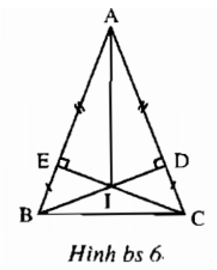
(A) 2;    (B) 3    (C) 4    (D) 5;

Hãy chọn đáp án đúng

Lời giải:

Chọn D. Năm cặp tam giác bằng nhau là:

ΔAEI = ΔADI, ΔBEI = ΔCDI, ΔAIB = ΔAIC, ΔBEC = ΔCDE, ΔABD = ΔACE.

Bài II.2: Cho hình bs 7. Chứng minh rằng OA = OB

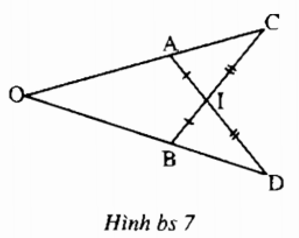
Lời giải:

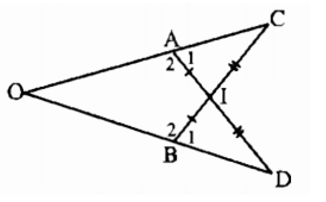
ΔAIC = ΔBID (c.g.c) suy ra ∠C = ∠D, ∠A₁ = ∠B₁, do đó ∠A₂ = ∠B₂.

ΔOAD = ΔOBC (g.c.g) suy ra OA = OB.

Bài II.3: Cho tam giác ABC cân tại A. Trên Tia đối của tia BA lấy điểm D, trên tia đối của tia CA lấy điểm E sao cho BD = CE. Gọi I là giao điểm của BE và CD

a) Chứng minh rằng IB = IC, ID = IE.

b) Chứng minh rằng BC song song DE.

c) Gọi M là trung điểm BC . Chứng minh rằng ba điểm A, M, I thẳng hàng.

Lời giải:

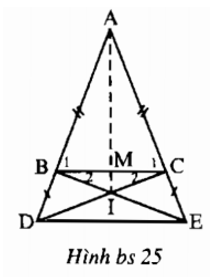
a) ΔABE = ΔACD (c.g.c)

suy ra BE = CD     (1)

và ∠ABE = ∠ACD.     (2)

Tam giác ABC cân nên ∠B₁ = ∠C₁.     (3)

Từ (2) và (3) suy ra

∠ABE - ∠B₁ = ∠ACD - ∠C₁, tức là ∠B₂ = ∠C₂.

Vậy ΔBIC cân, suy ra IB = IC.     (4)

Từ (1) và (4) suy ra BE = IB = CD – IC, tức là IE = ID.

b) Các tam giác cân ABC và ADC có chung góc ở đỉnh ∠A nên ∠B1 = ∠ADE, suy ra BC // DE.

c) Hãy chứng minh ∠AMB = 90°, ∠IMB = 90°.