Bài 105, 106, 107, 108, 109, 110 trang 153 SBT Toán 7 tập 1

Bài 105, 106, 107, 108, 109, 110 trang 153 SBT Toán 7 tập 1

Bài 105: Cho hình dưới trong đó AE ⊥BC. Tính AB biết AE = 4m; AC = 5m; BC = 9m

Lời giải:

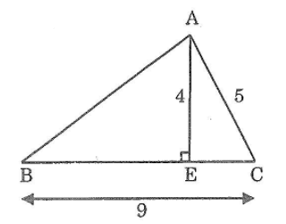
Áp dụng định lý pitago vào tam giác vuông AEC ta có:

AC² = AE² + EC²

⇒ EC² = AC² - AE² = 5² - 4² = 25 - 16 = 9

⇒ EC = 3M

Ta có: BC = BE + EC

BE = BC – EC = 9 – 3 = 6(m)

Áp dụng định lí pitago vào tam giác vuông AEB, ta có:

AB² = AE² + EB² = 4² + 6² = 16 + 36 = 52

Suy ra: AB = √52(m) ≈ 7,2m

Bài 106: Tìm các tam giác bằng nhau trong hình bên

Lời giải:

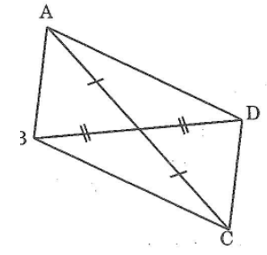
Ta có: ΔACB = ΔECD(c.g.c)

ΔABD = ΔEDB (c.c.c)

ΔABE = ΔEDA (c.c.c)

Bài 107: Tìm các tam giác cân trên hình dưới

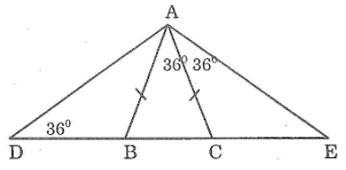
Lời giải:

Ta có: AB = AC (gt) nên ΔABC cân tại A

Trong ΔDAC , ta có:

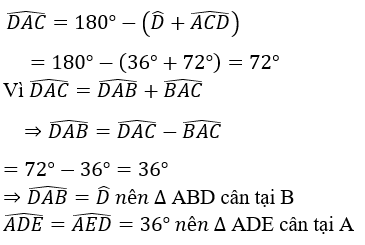
Vậy có 6 tam giác cân trong hình bên.

Bài 108: Bạn Mai vẽ tia phân giác của một góc như sau: đánh dấu trên hai cạnh của bốn góc bốn đoạn thẳng bằng nhau: OA = AB = OC + CD (hình dưới). kẻ các đoạn AD, BC chúng cắt nhau ở K. Hãy giải thích vì sao OK là tia phân giác của góc O.

Hướng dẫn: chứng minh rằng:

a. ΔOAD = ΔOCB

b. ΔKAB = ΔKCD

Lời giải:

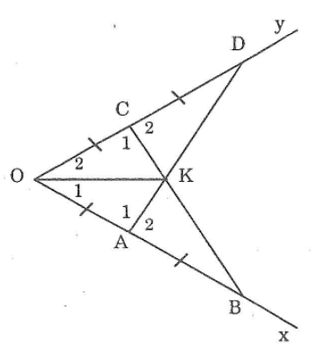
Xét ΔOAD và ΔOCB. Ta có:

OA = OC (gt)

∠O chung

OD = OB(gt)

Suy ra: ΔOAD = ΔOCB (c.g.c)

Ta có: ΔOAD = ΔOCB

Suy ra: D = B (hai góc tương ứng)

∠C₁ = ∠A₁ (hai góc tương ứng)

Lại có: ∠C₁ + ∠C₂ = 180° (hai góc kề bù)

∠A₁ + ∠A₂ = 180° (hai góc kề bù)

Suy ra: ∠C₂ = ∠A₂

Xét ΔKCD và ΔKAB, ta có:

B = D (chứng minh trên )

CD = AB (gt)

∠C₂ = ∠A₂ (chứng minh trên)

suy ra: ΔKCD = ΔKAB (g.c.g)

⇒ KC = KA (hai cạnh tương ứng)

Xét ΔOCK và ΔOAK, ta có:

OC = OA (gt)

OK chung

KA = KC (chứng minh trên)

Suy ra: ΔKCD = ΔKAB (c.c.c)

⇒ ∠O₁ = ∠O₂ (hai góc tương ứng)

Vậy OK là tia phân giác góc O

Bài 109: Cho tam giác ABC cân tại A, kẻ BH ⊥ AC. Gọi D là một điểm thuộc cạnh đáy BC. Kẻ DE ⊥ AC, DE ⊥ AB.

Chứng minh rằng DE + DF = BH

Lời giải:

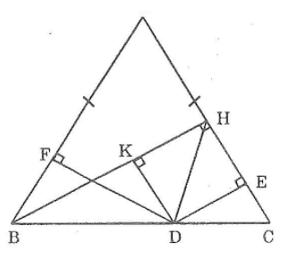
Kẻ DK ⊥ BH

Ta có: BH ⊥ AC(gt)

Suy ra: DK // AC (hai đường thẳng cùng vuông góc với đường thẳng thứ ba thì song song)

⇒ ∠KDB = C (hai góc đồng vị)

VìΔABC cân tại A nên ∠B = ∠C (tính chất tam giác cân)

Suy ra: ∠KDB = B

Xét hai tam giác vuông BFD và DKB, ta có:

∠BFD = ∠DKB

BD cạnh huyền chung

∠FBD = ∠KDB (chứng minh trên)

Suy ra:ΔBFD = ΔDKB (cạnh huyền góc nhọn)

⇒ DF = BK (hai cạnh tương ứng)     (1)

Nối DH. XétΔDEH và ΔDKH ta có:

∠DEH = ∠DKH = 90°

DH cạnh huyền chung

∠EHD = ∠KDH (hai góc so le trong)

Suy ra:ΔDEH = ΔDKH ( cạnh huyền , góc nhọn)

Suy ra: DE = HK ( hai cạnh tương ứng)     (2)

Mặt khác : BH = BK + KH (3)

Từ (1), (2) và (3) suy ra: DF = DE = BH

Bài 110: Cho tam giác ABC vuông tại A có AB/AC = 3/4 và BC = 15cm. Tính độ dài AB, AC

Lời giải:

Theo đề bài ta có:

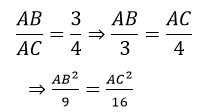
Theo tính chất dãy tỉ số bằng mhau ta có:

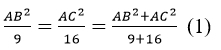
tam giác ABC vuông tại A

Áp dụng định lí pitago vào tam giác ABC ta có:

BC² = AB² + AC²     (2)

Từ (1) và (2) suy ra:

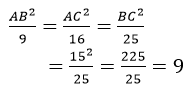
AB² = 9.9 = 81 ⇒ AB = 9 cm (vì AB > 0)

AC² = 16.9 = 144 ⇒ AB = 12 cm (vì AB > 0)