Bài 103, 104 trang 152 SBT Toán 7 tập 1

Bài 103, 104 trang 152 SBT Toán 7 tập 1

Bài 103: Cho đoạn thẳng AB. Vẽ các cung tâm A và B có cùng bán kính sao cho chúng cắt nhau tại C và D. chứng minh rằng CD là đường trung trực của AB.

Lời giải:

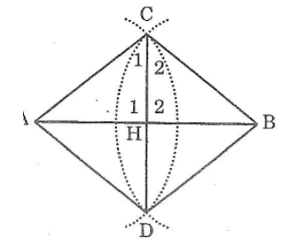
Gọi H là giao điểm của AB và CD

Nối AC, AD,BC,BD

Xét ΔACD và ΔBCD, ta có:

AC = BC

(bán kính hai cung tròn bằng nhau)

AD = BD

CD cạnh chung

Suy ra: ΔACD = ΔBCD (c.c.c)

Suy ra: ∠C₁ = ∠C₂ (hai góc tương ứng)

Xét hai tam giác AHC và BHC. Ta có:

AC = BC (bán kính hai cung tròn bằng nhau)

∠C₁ = ∠C₂ (chứng minh trên)

CH cạnh chung

Suy ra: ΔAHC = ΔBHC(c.g.c)

Suy ra: AH = BH (hai cạnh tương ứng)     (1)

Ta có : ∠H₁ = ∠H₂ (hai góc tương ứng)

∠H₁ + ∠H₂ = 180° (hai góc kề bù)

Suy ra: ∠H₁ = ∠H₂ = 90° ⇒ CD ⊥ AB     (2)

Từ (1) và (2) suy ra CD là đường trung trực của AB

Bài 104: Cho tam giác ADE cân tại A. Trên cạnh DE lấy các điểm B và C sao cho DB = EC = 1/2 DE

a. Tam giác ABC là tam giác gì? Chứng minh điều đó?

b. Kẻ BM ⊥ AD, kẻ CN ⊥ AE. Chứng minh rằng BM = CN

c. Gọi I là giao điểm của MB và NC. Tam giác IBC là tam giác gì? Chứng minh điều đó?

d. Chứng minh rằng AI là tia phân giác của góc BAC

Lời giải:

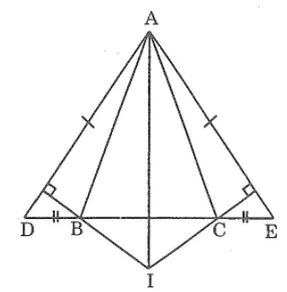
ΔADE cân tại A nên ∠D = ∠E

Xét ΔABD và ΔACE, ta có:

AD = AE (gt)

∠D = ∠E (chứng minh trên)

DB = EC (gt)

Suy ra: ΔABD = ΔACE (c.g.c)

Suy ra: AB = AC (hai cạnh tương ứng)

Vậy: ΔABC cân tại A

Xét hai tam giác vuông BMD và CNE, ta có:

(BMD) = (CNE) = 90°

BD = CE (gt)

∠D = ∠E (chứng minh trên)

Suy ra: ΔBMD = ΔCNE (cạnh huyền,góc nhọn)

Ta có: ΔBMD = ΔCNE (chứng minh trên)

Suy ra: ∠DBM = ∠ECN (hai góc tương ứng)

∠DBM = ∠IBC (đối đỉnh)

∠ECN = ∠ICB (đối đỉnh)

Suy ra: ∠IBC = ∠ICB hay ΔIBC cân tại I

Xét ΔABI và ΔACI, ta có:

AB = AC (chứng minh trên)

IB = IC ( vì ΔIBC cân tại I)

AI cạnh chung

Suy ra: ΔABI = ΔACI(c.c.c) ⇒ ∠BAI = ∠CAI (hai góc tương ứng)

Vậy AI là tia phân giác của góc ∠BAC