Bài 19, 20, 21, 22, 23 trang 40 SBT Toán 7 tập 2

Bài 19, 20, 21, 22, 23 trang 40 SBT Toán 7 tập 2

Bài 19: Có thể có tam giác nào mà độ dài ba cạnh như sau không?

a. 5cm; 10cm; 12cm?

b. 1m; 2m; 3,3cm?

c. 1,2m; 1m; 2,2m?

Lời giải:

a. Ta có: 5 + 10 > 12

            5 + 12 > 10

            10 + 12 > 5

Vậy có tam giác mà ba cạnh của nó là 5cm; 10cm; 12cm.

b. Ta có: 1 + 2 < 3,3

Không có tam giác mà ba cạnh của nó là 1cm; 2m; 3,3m vì tổng hai cạnh nhỏ hơn cạnh còn lại.

c. Ta có: 1,2 + 1 = 2,2

Không có tam giác mà ba cạnh của nó là 1,2m; 1m; 2,2m vì tổng hai cạnh bằng cạnh còn lại.

Bài 20: Cho tam giác ABC có AB = 4cm, AC = 1cm. Hãy tìm độ dài cạnh BC biết rằng độ dài này là một số nguyên (cm).

Lời giải:

Theo bất đẳng thức tam giác và hệ quả ta có:

            AB - AC < BC < AB + AC    (1)

Thay AB = 4cm, AC = 1cm vào (1) ta có:

            4 - 1 < BC 4 + 1 ⇔ 3 < BC < 5

Vì độ dài cạnh BC là một số nguyên nên BC = 4cm.

Bài 21: Cho hình bên. Chứng minh rằng: MA + MB < IA + IB < CA + CB

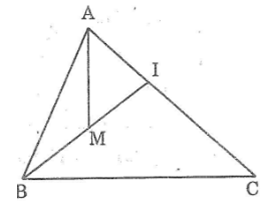
Lời giải:

Trong ΔAMI ta có:

MA < MI + IA

(theo bất đẳng thức tam giác)

Cộng vào hai vế với MB ta có:

MA + MB < MI + IA + MB

⇒ MA + MB < IB + IA    (1)

Trong ΔBIC, ta có:

IB < IC + CB (bất đẳng thức tam giác)

Cộng vào 2 vế với IA ta có:

IB + IA < IC + CB + IA

⇒ IB + IA < CA + CB    (2)

Từ (1) và (2) suy ra: MA + MB < IA + IB < CA + CB.

Bài 22: Tính chu vi của một tam giác cân có hai cạnh bằng 4m và 9m.

Lời giải:

Ta có: 4 + 4 < 9 nên cạnh 4m không thể là cạnh bên (vì nếu cạnh bên là 4m thì trái với bất đẳng thức tam giác)

Suy ra cạnh 4m là cạnh đáy, cạnh 9m là cạnh bên.

Chu vi của tam giác là: 4 + 9 + 9 = 22 (m).

Bài 23: Cho tam giác ABC trong đó BC là cạnh lớn nhất.

a. Vì sao các góc B và C không thể là góc vuông hoặc góc tù?

b. Gọi AH là đường vuông góc kẻ từ A đến BC. So sánh AB + AC với BH + CH rồi chứng minh rằng AB + AC > BC.

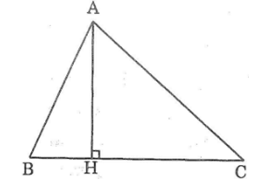
Lời giải:

a. *Giả sử ∠B ≥ 90°

Vì trong một tam giác cạnh đối diện với góc vuông hoặc góc tù là cạnh lớn nhất nên AC > BC.

Điều này trái với giả thiết cạnh BC là cạnh lớn nhất.

*Giả sử ∠C ≥ 90°

Vì trong một tam giác cạnh đối diện với góc vuông hoặc góc tù là cạnh lớn nhất nên AB > BC.

Điều này trái với giả thiết cạnh BC là cạnh lớn nhất.

Vậy ∠B và ∠C không thể là góc vuông hoặc góc tù (là các góc nhọn).

b. Vì điểm H nằm giữa B và C nên ta có: BH + HC = BC    (1)

Lại có: AB > BH (đường xiên lớn hơn đường vuông góc)

AC > CH (đường xiên lớn hơn đường vuông góc)

Cộng từng vế ta có: AB + AC > BH + CH    (2)

Từ (1) và (2) suy ra: AB + AC > BC